Problem

The Magnet (“Magnets”) puzzle involves placing domino-shaped magnets (each with a + and - pole) into predefined paired slots on a rectangular grid so that all given numerical constraints are satisfied.

Board cells are partitioned into domino slots (horizontal or vertical). Each domino must be assigned either (+, -) or (-, +) according to orientation, or left unused (X X). Additional global constraints:

  1. Row / column counts: Arrays top[], bottom[], left[], right[] specify how many + or - signs must appear in each column or row (with -1 meaning unconstrained). top[j] counts + in column j; bottom[j] counts - in column j; similarly for left[i] (pluses in row i) and right[i] (minuses in row i).
  2. Adjacency: No two orthogonally adjacent cells may contain the same sign (+ next to + or - next to -). Diagonals are allowed to match.
  3. Domino structure: Orientation matrix rules gives for each slot-end one of L, R, T, B (left/right or top/bottom half); valid dominoes are (L,R) horizontally adjacent or (T,B) vertically adjacent pairs.
  4. Each domino slot may be unused (both cells marked X).

Goal: Assign polarities (or unused) to all slots so that all constraints hold; output one valid filled board (or report unsolvable).

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

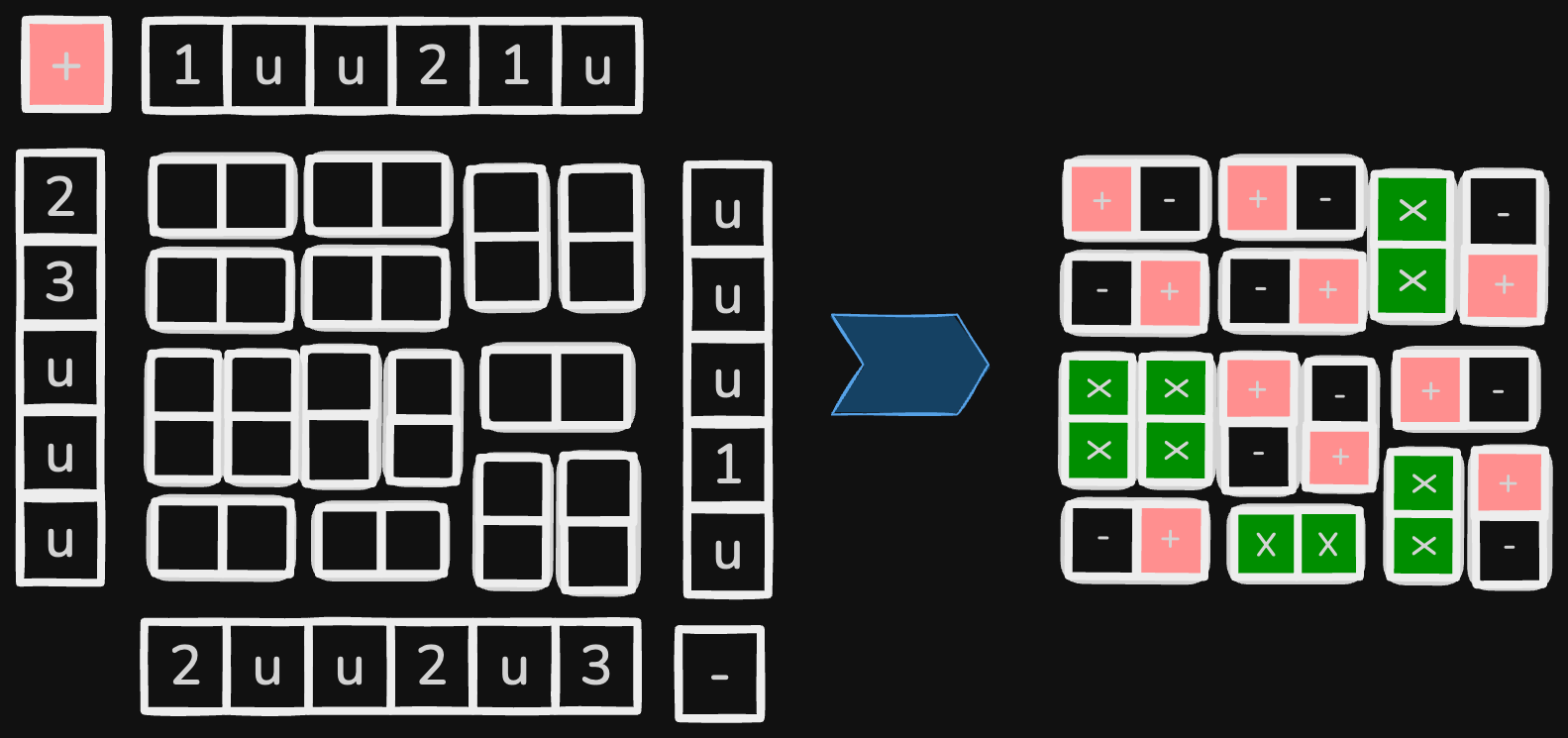
Input : M = 5, N = 6
 top[] = [1, -1, -1, 2, 1, -1]
 bottom[] = [2, -1, -1, 2, -1, 3]
 left[] = [2, 3, -1, -1, -1]
 right[] = [-1, -1, -1, 1, -1]
 rules[][] = [[L, R, L, R, T, T],
 [L, R, L, R, B, B],
 [T, T, T, T, L, R],
 [B, B, B, B, T, T],
 [L, R, L, R, B, B]];
Output : 
 + - + - X -
 - + - + X +
 X X + - + -
 X X - + X +
 - + X X X -

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

Input : M = 4, N = 3
 top[] = [2, -1, -1]
 bottom[] = [-1, -1, 2]
 left[] = [-1, -1, 2, -1]
 right[] = [0, -1, -1, -1]
 rules[][] = [[T, T, T],
 [B, B, B],
 [T, L, R],
 [B, L, R]];
Output : 
 + X +
 – X –
 + – +
 – + –

Constraints

  • Typical puzzle sizes: M, N <= 8..10 (practical backtracking limit)
  • Number of domino slots derived from rules layout.
  • Sum feasibility: For each row/col with constraint c for + (or -), must have enough available cells in that row/col to reach c.

Solution

Method 1 - Backtracking with Incremental Constraint Pruning

Intuition

The search space is all assignments of each domino slot to one of three states: (+, -), (-, +) or unused (X, X). We prune early when:

  1. A row/col already exceeds its + / - quota.
  2. Remaining unfilled cells in a row/col are insufficient to reach a still-needed quota.
  3. Adjacency rule would be violated by placing a polarity at a cell.

By scanning the grid cell-by-cell in a deterministic order and branching only at canonical slot starts (L or T), we avoid duplicate work.

Approach

  1. Pre-parse rules to identify domino slot starts (cells marked L or T).
  2. Maintain counters:
    • plusRow[i], minusRow[i], plusCol[j], minusCol[j].
  3. Recursive function dfs(idx) where idx enumerates domino slots:
    • For each slot (two coordinates a, b), try states:
    • (+, -) if both legal.
    • (-, +) if both legal.
    • X X (skip) always legal (but keep for solution existence; can be pruned if quotas require filling).
    • Before recursing, check row/col quota feasibility (no overfill; capacity remaining sufficient).
  4. Stop at first complete assignment satisfying all exact quotas (where specified; unconstrained quotas ignored).
  5. Use adjacency checks on-the-fly (constant time around the two modified cells).

Pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

build list slots from rules where cell is 'L' or 'T'
initialize counts to 0; fill quotas arrays top, bottom, left, right

def feasible_after(place):
  # check not exceeding quota and enough remaining cells to still meet quota
  return rows_ok and cols_ok

def try_state(slot, pattern):  # pattern in {(+, -), (-, +), (X, X)}
  check adjacency for each non-X cell
  apply updates to board + counters
  if feasible_after: dfs(next)
  revert

def dfs(k):
  if k == len(slots): return all exact quotas satisfied
  slot = slots[k]
  for pattern in [(+, -), (-, +), (X,X)]:
    try_state(slot, pattern)
  return false

dfs(0)

Code

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164

#include <array>

// Refactored: provides a Solution class returning the solved board instead of printing.
// Google style: types in PascalCase, functions/variables in lowerCamelCase, no using-directives.

class Solution {
 public:
  static constexpr int kRows = 5;
  static constexpr int kCols = 6;
  using Board = std::array<std::array<char, kCols>, kRows>;

  Board solve(const std::array<int, kCols>& topQuota,
              const std::array<int, kCols>& bottomQuota,
              const std::array<int, kRows>& leftQuota,
              const std::array<int, kRows>& rightQuota,
              const Board& slotRules) {
    Board board{};
    for (int r = 0; r < kRows; ++r) {
      for (int c = 0; c < kCols; ++c) {
        board[r][c] = 'X';
      }
    }
    backtrack(board, 0, 0, topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    return board; // If unsolvable, remains 'X'.
  }

 private:
  bool backtrack(Board& board, int row, int col,
                 const std::array<int, kCols>& topQuota,
                 const std::array<int, kCols>& bottomQuota,
                 const std::array<int, kRows>& leftQuota,
                 const std::array<int, kRows>& rightQuota,
                 const Board& slotRules) {
    if (row >= kRows - 1 && col >= kCols - 1) {
      return validate(board, topQuota, bottomQuota, leftQuota, rightQuota);
    }
    if (col >= kCols) {
      col = 0;
      ++row;
    }
    if (row >= kRows) {
      return false;
    }
    char cell = slotRules[row][col];
    if (cell == 'R' || cell == 'B') {
      return backtrack(board, row, col + 1, topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    }

    // Horizontal domino start (L,R)
    if (cell == 'L' && col + 1 < kCols && slotRules[row][col + 1] == 'R') {
      tryAssign(board, row, col, row, col + 1, '+', '-', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
      tryAssign(board, row, col, row, col + 1, '-', '+', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    }
    // Vertical domino start (T,B)
    if (cell == 'T' && row + 1 < kRows && slotRules[row + 1][col] == 'B') {
      tryAssign(board, row, col, row + 1, col, '+', '-', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
      tryAssign(board, row, col, row + 1, col, '-', '+', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    }
    // Option: leave cells unused ('X'), move forward.
    return backtrack(board, row, col + 1, topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
  }

  void tryAssign(Board& board, int r1, int c1, int r2, int c2,
                 char ch1, char ch2,
                 const std::array<int, kCols>& topQuota,
                 const std::array<int, kCols>& bottomQuota,
                 const std::array<int, kRows>& leftQuota,
                 const std::array<int, kRows>& rightQuota,
                 const Board& slotRules) {
    if (!isSafe(board, r1, c1, ch1, topQuota, bottomQuota, leftQuota, rightQuota) ||
        !isSafe(board, r2, c2, ch2, topQuota, bottomQuota, leftQuota, rightQuota)) {
      return;
    }
    board[r1][c1] = ch1;
    board[r2][c2] = ch2;
    if (backtrack(board, r1, c1 + 1, topQuota, bottomQuota, leftQuota, rightQuota, slotRules)) {
      return; // success path retains assignment
    }
    board[r1][c1] = 'X';
    board[r2][c2] = 'X';
  }

  bool isSafe(const Board& board, int row, int col, char ch,
              const std::array<int, kCols>& topQuota,
              const std::array<int, kCols>& bottomQuota,
              const std::array<int, kRows>& leftQuota,
              const std::array<int, kRows>& rightQuota) const {
    if ((row - 1 >= 0 && board[row - 1][col] == ch) ||
        (col + 1 < kCols && board[row][col + 1] == ch) ||
        (row + 1 < kRows && board[row + 1][col] == ch) ||
        (col - 1 >= 0 && board[row][col - 1] == ch)) {
      return false;
    }
    int rowPlus = (ch == '+') ? countRow(board, row, '+') : 0;
    int rowMinus = (ch == '-') ? countRow(board, row, '-') : 0;
    int colPlus = (ch == '+') ? countCol(board, col, '+') : 0;
    int colMinus = (ch == '-') ? countCol(board, col, '-') : 0;
    if (ch == '+') {
      if (topQuota[col] != -1 && colPlus >= topQuota[col]) {
        return false;
      }
      if (leftQuota[row] != -1 && rowPlus >= leftQuota[row]) {
        return false;
      }
    } else {
      if (bottomQuota[col] != -1 && colMinus >= bottomQuota[col]) {
        return false;
      }
      if (rightQuota[row] != -1 && rowMinus >= rightQuota[row]) {
        return false;
      }
    }
    return true;
  }

  int countRow(const Board& board, int row, char ch) const {
    int cnt = 0;
    for (int c = 0; c < kCols; ++c) {
      if (board[row][c] == ch) ++cnt;
    }
    return cnt;
  }
  int countCol(const Board& board, int col, char ch) const {
    int cnt = 0;
    for (int r = 0; r < kRows; ++r) {
      if (board[r][col] == ch) ++cnt;
    }
    return cnt;
  }

  bool validate(const Board& board,
                const std::array<int, kCols>& topQuota,
                const std::array<int, kCols>& bottomQuota,
                const std::array<int, kRows>& leftQuota,
                const std::array<int, kRows>& rightQuota) const {
    for (int c = 0; c < kCols; ++c) {
      if (topQuota[c] != -1 && countCol(board, c, '+') != topQuota[c]) {
        return false;
      }
    }
    for (int r = 0; r < kRows; ++r) {
      if (leftQuota[r] != -1 && countRow(board, r, '+') != leftQuota[r]) {
        return false;
      }
    }
    for (int c = 0; c < kCols; ++c) {
      if (bottomQuota[c] != -1 && countCol(board, c, '-') != bottomQuota[c]) {
        return false;
      }
    }
    for (int r = 0; r < kRows; ++r) {
      if (rightQuota[r] != -1 && countRow(board, r, '-') != rightQuota[r]) {
        return false;
      }
    }
    return true;
  }
};

// Usage example (pseudo):
// Solution::Board rules = { /* fill with 'L','R','T','B' layout */ };
// std::array<int, Solution::kCols> top = {1,-1,-1,2,1,-1};
// ... fill other arrays ...
// Solution sol; auto board = sol.solve(top, bottom, left, right, rules);

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131

// Refactored Java version: Solution class returning a char[][] board.
public class Solution {
  public static final int K_ROWS = 5;
  public static final int K_COLS = 6;

  public char[][] solve(int[] topQuota, int[] bottomQuota, int[] leftQuota, int[] rightQuota, char[][] slotRules) {
    char[][] board = new char[K_ROWS][K_COLS];
    for (int r = 0; r < K_ROWS; ++r) {
      for (int c = 0; c < K_COLS; ++c) {
        board[r][c] = 'X';
      }
    }
    backtrack(board, 0, 0, topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    return board; // remains 'X' if unsolvable
  }

  private boolean backtrack(char[][] board, int row, int col,
                            int[] topQuota, int[] bottomQuota, int[] leftQuota, int[] rightQuota,
                            char[][] slotRules) {
    if (row >= K_ROWS - 1 && col >= K_COLS - 1) {
      return validate(board, topQuota, bottomQuota, leftQuota, rightQuota);
    }
    if (col >= K_COLS) {
      col = 0;
      ++row;
    }
    if (row >= K_ROWS) {
      return false;
    }
    char cell = slotRules[row][col];
    if (cell == 'R' || cell == 'B') {
      return backtrack(board, row, col + 1, topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    }

    if (cell == 'L' && col + 1 < K_COLS && slotRules[row][col + 1] == 'R') {
      tryAssign(board, row, col, row, col + 1, '+', '-', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
      tryAssign(board, row, col, row, col + 1, '-', '+', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    }
    if (cell == 'T' && row + 1 < K_ROWS && slotRules[row + 1][col] == 'B') {
      tryAssign(board, row, col, row + 1, col, '+', '-', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
      tryAssign(board, row, col, row + 1, col, '-', '+', topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
    }
    return backtrack(board, row, col + 1, topQuota, bottomQuota, leftQuota, rightQuota, slotRules);
  }

  private void tryAssign(char[][] board, int r1, int c1, int r2, int c2,
                         char ch1, char ch2,
                         int[] topQuota, int[] bottomQuota, int[] leftQuota, int[] rightQuota,
                         char[][] slotRules) {
    if (!isSafe(board, r1, c1, ch1, topQuota, bottomQuota, leftQuota, rightQuota) ||
        !isSafe(board, r2, c2, ch2, topQuota, bottomQuota, leftQuota, rightQuota)) {
      return;
    }
    board[r1][c1] = ch1;
    board[r2][c2] = ch2;
    if (backtrack(board, r1, c1 + 1, topQuota, bottomQuota, leftQuota, rightQuota, slotRules)) {
      return;
    }
    board[r1][c1] = 'X';
    board[r2][c2] = 'X';
  }

  private boolean isSafe(char[][] board, int row, int col, char ch,
                         int[] topQuota, int[] bottomQuota, int[] leftQuota, int[] rightQuota) {
    if ((row - 1 >= 0 && board[row - 1][col] == ch) ||
        (col + 1 < K_COLS && board[row][col + 1] == ch) ||
        (row + 1 < K_ROWS && board[row + 1][col] == ch) ||
        (col - 1 >= 0 && board[row][col - 1] == ch)) {
      return false;
    }
    int rowPlus = (ch == '+') ? countRow(board, row, '+') : 0;
    int rowMinus = (ch == '-') ? countRow(board, row, '-') : 0;
    int colPlus = (ch == '+') ? countCol(board, col, '+') : 0;
    int colMinus = (ch == '-') ? countCol(board, col, '-') : 0;
    if (ch == '+') {
      if (topQuota[col] != -1 && colPlus >= topQuota[col]) {
        return false;
      }
      if (leftQuota[row] != -1 && rowPlus >= leftQuota[row]) {
        return false;
      }
    } else {
      if (bottomQuota[col] != -1 && colMinus >= bottomQuota[col]) {
        return false;
      }
      if (rightQuota[row] != -1 && rowMinus >= rightQuota[row]) {
        return false;
      }
    }
    return true;
  }

  private int countRow(char[][] board, int row, char ch) {
    int cnt = 0;
    for (int c = 0; c < K_COLS; ++c) {
      if (board[row][c] == ch) ++cnt;
    }
    return cnt;
  }
  private int countCol(char[][] board, int col, char ch) {
    int cnt = 0;
    for (int r = 0; r < K_ROWS; ++r) {
      if (board[r][col] == ch) ++cnt;
    }
    return cnt;
  }

  private boolean validate(char[][] board, int[] topQuota, int[] bottomQuota, int[] leftQuota, int[] rightQuota) {
    for (int c = 0; c < K_COLS; ++c) {
      if (topQuota[c] != -1 && countCol(board, c, '+') != topQuota[c]) {
        return false;
      }
    }
    for (int r = 0; r < K_ROWS; ++r) {
      if (leftQuota[r] != -1 && countRow(board, r, '+') != leftQuota[r]) {
        return false;
      }
    }
    for (int c = 0; c < K_COLS; ++c) {
      if (bottomQuota[c] != -1 && countCol(board, c, '-') != bottomQuota[c]) {
        return false;
      }
    }
    for (int r = 0; r < K_ROWS; ++r) {
      if (rightQuota[r] != -1 && countRow(board, r, '-') != rightQuota[r]) {
        return false;
      }
    }
    return true;
  }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

from typing import List

class Solution:
  k_rows = 5
  k_cols = 6

  def solve(self, top_quota: List[int], bottom_quota: List[int], left_quota: List[int], right_quota: List[int], slot_rules: List[List[str]]) -> List[List[str]]:
    board = [['X' for _ in range(self.k_cols)] for _ in range(self.k_rows)]
    self.backtrack(board, 0, 0, top_quota, bottom_quota, left_quota, right_quota, slot_rules)
    return board

  def backtrack(self, board: List[List[str]], row: int, col: int, top_quota: List[int], bottom_quota: List[int], left_quota: List[int], right_quota: List[int], slot_rules: List[List[str]]) -> bool:
    if row >= self.k_rows - 1 and col >= self.k_cols - 1:
      return self.validate(board, top_quota, bottom_quota, left_quota, right_quota)
    if col >= self.k_cols:
      col = 0
      row += 1
    if row >= self.k_rows:
      return False
    cell = slot_rules[row][col]
    if cell in ('R', 'B'):
      return self.backtrack(board, row, col + 1, top_quota, bottom_quota, left_quota, right_quota, slot_rules)

    if cell == 'L' and col + 1 < self.k_cols and slot_rules[row][col + 1] == 'R':
      if self.try_assign(board, row, col, row, col + 1, '+', '-', top_quota, bottom_quota, left_quota, right_quota, slot_rules):
        return True
      if self.try_assign(board, row, col, row, col + 1, '-', '+', top_quota, bottom_quota, left_quota, right_quota, slot_rules):
        return True
    if cell == 'T' and row + 1 < self.k_rows and slot_rules[row + 1][col] == 'B':
      if self.try_assign(board, row, col, row + 1, col, '+', '-', top_quota, bottom_quota, left_quota, right_quota, slot_rules):
        return True
      if self.try_assign(board, row, col, row + 1, col, '-', '+', top_quota, bottom_quota, left_quota, right_quota, slot_rules):
        return True
    return self.backtrack(board, row, col + 1, top_quota, bottom_quota, left_quota, right_quota, slot_rules)

  def try_assign(self, board, r1, c1, r2, c2, ch1, ch2, top_quota, bottom_quota, left_quota, right_quota, slot_rules):
    if not self.is_safe(board, r1, c1, ch1, top_quota, bottom_quota, left_quota, right_quota) or not self.is_safe(board, r2, c2, ch2, top_quota, bottom_quota, left_quota, right_quota):
      return False
    board[r1][c1] = ch1
    board[r2][c2] = ch2
    if self.backtrack(board, r1, c1 + 1, top_quota, bottom_quota, left_quota, right_quota, slot_rules):
      return True
    board[r1][c1] = 'X'
    board[r2][c2] = 'X'
    return False

  def is_safe(self, board, row, col, ch, top_quota, bottom_quota, left_quota, right_quota):
    if (row - 1 >= 0 and board[row - 1][col] == ch) or (col + 1 < self.k_cols and board[row][col + 1] == ch) or (row + 1 < self.k_rows and board[row + 1][col] == ch) or (col - 1 >= 0 and board[row][col - 1] == ch):
      return False
    row_plus = self.count_row(board, row, '+') if ch == '+' else 0
    row_minus = self.count_row(board, row, '-') if ch == '-' else 0
    col_plus = self.count_col(board, col, '+') if ch == '+' else 0
    col_minus = self.count_col(board, col, '-') if ch == '-' else 0
    if ch == '+':
      if top_quota[col] != -1 and col_plus >= top_quota[col]:
        return False
      if left_quota[row] != -1 and row_plus >= left_quota[row]:
        return False
    else:
      if bottom_quota[col] != -1 and col_minus >= bottom_quota[col]:
        return False
      if right_quota[row] != -1 and row_minus >= right_quota[row]:
        return False
    return True

  def count_row(self, board, row, ch):
    return sum(1 for c in range(self.k_cols) if board[row][c] == ch)

  def count_col(self, board, col, ch):
    return sum(1 for r in range(self.k_rows) if board[r][col] == ch)

  def validate(self, board, top_quota, bottom_quota, left_quota, right_quota):
    for c in range(self.k_cols):
      if top_quota[c] != -1 and self.count_col(board, c, '+') != top_quota[c]:
        return False
    for r in range(self.k_rows):
      if left_quota[r] != -1 and self.count_row(board, r, '+') != left_quota[r]:
        return False
    for c in range(self.k_cols):
      if bottom_quota[c] != -1 and self.count_col(board, c, '-') != bottom_quota[c]:
        return False
    for r in range(self.k_rows):
      if right_quota[r] != -1 and self.count_row(board, r, '-') != right_quota[r]:
        return False
    return True

Complexity

  • ⏰ Time complexity: O(3^S) in the worst case where S is the number of domino slots (each slot has up to 3 choices). Pruning (quota feasibility + adjacency + early overfill) dramatically reduces search; practical boards solve quickly.
  • 🧺 Space complexity: O(S + M*N) – recursion depth up to number of slots plus board & counter storage.