problemeasyalgorithmsleetcode-1582leetcode 1582leetcode1582

Special Positions in a Binary Matrix

EasyUpdated: Jul 26, 2025
Practice on:
LeetCode

Problem

Given an m x n binary matrix mat, return the number of special positions inmat .

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

Examples

Example 1

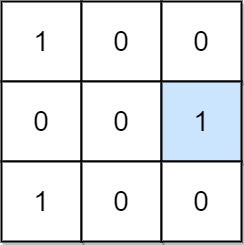
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2

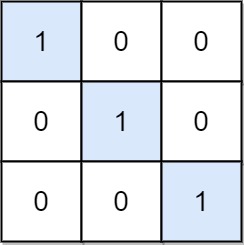
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

Constraints

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 100
  • mat[i][j] is either 0 or 1.

Solution

Method 1 – Row and Column Counting

Intuition

A position is special if it is the only 1 in its row and column. By counting the number of 1s in each row and column, we can quickly check for each cell if it is a special position.

Approach

  1. Count the number of 1s in each row and each column.
  2. For each cell, if it is 1 and both its row and column counts are 1, increment the answer.
  3. Return the total count of special positions.

Code

C++
#include <vector>
using namespace std;
class Solution {
public:
    int numSpecial(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<int> row(m), col(n);
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (mat[i][j]) { row[i]++; col[j]++; }
        int ans = 0;
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (mat[i][j] && row[i] == 1 && col[j] == 1) ans++;
        return ans;
    }
};
Go
func numSpecial(mat [][]int) int {
    m, n := len(mat), len(mat[0])
    row := make([]int, m)
    col := make([]int, n)
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if mat[i][j] == 1 {
                row[i]++
                col[j]++
            }
        }
    }
    ans := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if mat[i][j] == 1 && row[i] == 1 && col[j] == 1 {
                ans++
            }
        }
    }
    return ans
}
Java
class Solution {
    public int numSpecial(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[] row = new int[m], col = new int[n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (mat[i][j] == 1) { row[i]++; col[j]++; }
        int ans = 0;
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (mat[i][j] == 1 && row[i] == 1 && col[j] == 1) ans++;
        return ans;
    }
}
Kotlin
class Solution {
    fun numSpecial(mat: Array<IntArray>): Int {
        val m = mat.size
        val n = mat[0].size
        val row = IntArray(m)
        val col = IntArray(n)
        for (i in 0 until m)
            for (j in 0 until n)
                if (mat[i][j] == 1) {
                    row[i]++
                    col[j]++
                }
        var ans = 0
        for (i in 0 until m)
            for (j in 0 until n)
                if (mat[i][j] == 1 && row[i] == 1 && col[j] == 1) ans++
        return ans
    }
}
Python
class Solution:
    def numSpecial(self, mat: list[list[int]]) -> int:
        m, n = len(mat), len(mat[0])
        row = [0]*m
        col = [0]*n
        for i in range(m):
            for j in range(n):
                if mat[i][j] == 1:
                    row[i] += 1
                    col[j] += 1
        ans = 0
        for i in range(m):
            for j in range(n):
                if mat[i][j] == 1 and row[i] == 1 and col[j] == 1:
                    ans += 1
        return ans
Rust
impl Solution {
    pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut row = vec![0; m];
        let mut col = vec![0; n];
        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 1 {
                    row[i] += 1;
                    col[j] += 1;
                }
            }
        }
        let mut ans = 0;
        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 1 && row[i] == 1 && col[j] == 1 {
                    ans += 1;
                }
            }
        }
        ans
    }
}
TypeScript
class Solution {
    numSpecial(mat: number[][]): number {
        const m = mat.length, n = mat[0].length;
        const row = Array(m).fill(0), col = Array(n).fill(0);
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j)
                if (mat[i][j] === 1) {
                    row[i]++;
                    col[j]++;
                }
        let ans = 0;
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j)
                if (mat[i][j] === 1 && row[i] === 1 && col[j] === 1) ans++;
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(mn) – Each cell is visited twice, once for counting and once for checking.
  • 🧺 Space complexity: O(m+n) – For row and column counts.

Comments