Problem

Problem

Given an m x n matrix, return all elements of the matrix in spiral order.

Examples

Example 1:

Input: matrix = [
	[ 1, 2, 3 ],
	[ 4, 5, 6 ],
	[ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

Input: matrix =[[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

Follow Up

[Spiral Matrix 2 - Generate](spiral-matrix-2-generate)

Similar Problems

• [Spiral Matrix 2 - Generate](spiral-matrix-2-generate)
• [Spiral Matrix 3 - Traverse from Given Starting Point](spiral-matrix-3-traverse-from-given-starting-point)
• [Spiral Matrix 4 - From Linked List](spiral-matrix-4-from-linked-list)

Solution

Video explanation

Here is the video explaining below methods in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/u8XW5cR5djA" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Iterative just checking boundaries

We have 4 boundaries - left, right, top and bottom. We now have to loop from left to right, then top to bottom, then right to left and bottom to top. Each time, we change direction, we update respective boundary.

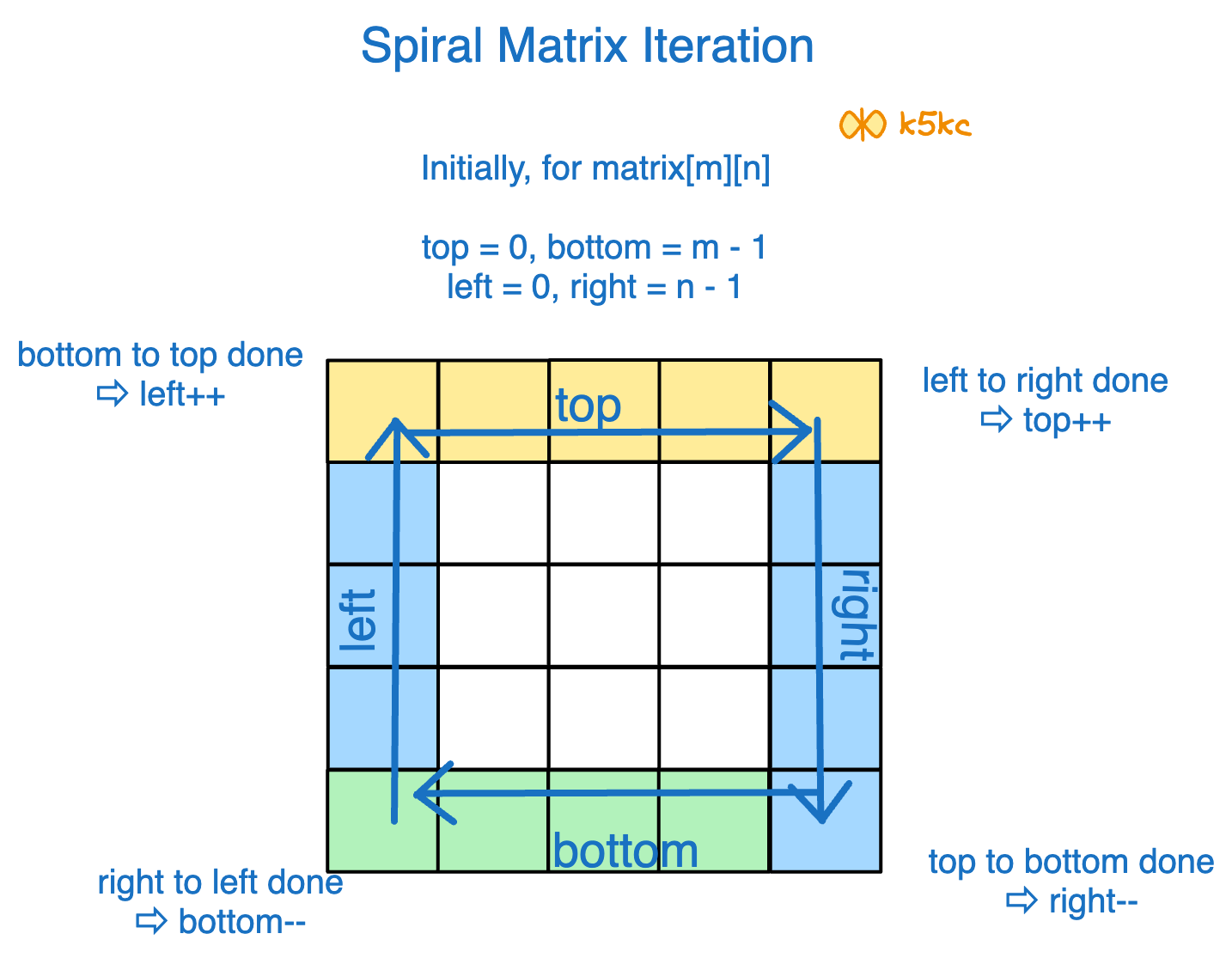
Also, we can run the loop in 2 ways:

while(left < right && top < bottom)

OR

while(ans.size() < m*n)

In the code below, we are using former, but any of the conditions will work.

Code

Java

public class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();

        // Define boundaries
        int top = 0;
        int bottom = matrix.length - 1;
        int left = 0;
        int right = matrix[0].length - 1;

        while (top <= bottom && left <= right) {
            // Traverse top row from left to right
            for (int j = left; j <= right; j++) {
                ans.add(matrix[top][j]);
            }
            top++;

            // Traverse right column from top to bottom
            for (int i = top; i <= bottom; i++) {
                ans.add(matrix[i][right]);
            }
            right--;

            // Traverse bottom row from right to left (if within bounds)
            if (top > bottom || left > right) {
                break;
            }
            for (int j = right; j >= left; j--) {
                ans.add(matrix[bottom][j]);
            }
            bottom--;


            // Traverse left column from bottom to top (if within bounds)
            for (int i = bottom; i >= top; i--) {
                ans.add(matrix[i][left]);
            }
            left++;
        }

        return ans;
    }
}

Python

class Solution:
    def spiralOrder(self, matrix: list[list[int]]) -> list[int]:
        ans: list[int] = []

        top: int = 0
        bottom: int = len(matrix) - 1
        left: int = 0
        right: int = len(matrix[0]) - 1

        while top <= bottom and left <= right:
            for j in range(left, right + 1):
                ans.append(matrix[top][j])
            top += 1

            for i in range(top, bottom + 1):
                ans.append(matrix[i][right])
            right -= 1

            if top > bottom or left > right:
                break
            
            for j in range(right, left - 1, -1):
                ans.append(matrix[bottom][j])
            bottom -= 1

            for i in range(bottom, top - 1, -1):
                ans.append(matrix[i][left])
            left += 1

        return ans

Complexity

• ⏰ Time complexity: O(m*n) where m is number of rows and n is number of columns.
• 🧺 Space complexity: O(1)

Method 2 - Iterative checking boundaries with stopping condition as element count

Same as method 1 with the stopping condition based on element count.

Code

Java

class Solution {
	public List<Integer> spiralOrder(int[][] matrix) {
		List<Integer> ans = new ArrayList<Integer> ();
		if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
			return ans;
		}
	
		int m = matrix.length;
		int n = matrix[0].length;
	
		int left = 0;
		int right = n - 1;
		int top = 0;
		int bottom = m - 1;
	
		while (ans.size() < m * n) {
			for (int i = left; i<= right; i++) {
				ans.add(matrix[top][i]);
			}
			top++;
	
			for (int i = top; i<= bottom; i++) {
				ans.add(matrix[i][right]);
			}
			right--;
	
			//prevent duplicate row
			if (top <= bottom) {
				for (int i = right; i >= left; i--) {
					ans.add(matrix[bottom][i]);
				}
				bottom--;
			}
	
			// prevent duplicate column
			if (left <= right) {
				for (int i = bottom; i >= top; i--) {
					ans.add(matrix[i][left]);
				}
				left++;
			}
		}
	
		return ans;
	}
}

Method 3 - Iterative with direction and switch case

Code

Java

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> ans = new ArrayList<>();
        if (matrix.length == 0 || matrix[0].length == 0) {
            return ans;
        }

        int top = 0;
        int bottom = matrix.length - 1;
        int left = 0;
        int right = matrix[0].length - 1;
        int dir = 0; // we go right, down, left, top

        while (top <= bottom && left <= right) {
            switch (dir) {
                case 0: // Right
                    for (int i = left; i <= right; i++) {
                        result.add(matrix[top][i]);
                    }
                    top++;
                    break;
                case 1: // Down
                    for (int i = top; i <= bottom; i++) {
                        result.add(matrix[i][right]);
                    }
                    right--;
                    break;
                case 2: // Left
                    for (int i = right; i >= left; i--) {
                        result.add(matrix[bottom][i]);
                    }
                    bottom--;
                    break;
                case 3: // Top
                    for (int i = bottom; i >= top; i--) {
                        result.add(matrix[i][left]);
                    }
                    left++;
            }
            dir = (dir + 1) % 4;
        }

        return result;
    }
}

Complexity

• ⏰ Time complexity: O(m*n)
• 🧺 Space complexity: O(1)

Method 4 - Recursive

Here is the logic:

• Start printing from first row.
• Print row and columns, forward and backward alternatively
• With every iteration of (either row or column), reduce the size of an row or column by 1
• Call recursively

We can also recursively solve this problem. The solution's performance is not better than Solution 1. Therefore, Solution 1 should be preferred.

Code

Java

class Solution {

	public List<Integer> spiralOrder(int[][] matrix) {
		List<Integer> ans = new ArrayList<Integer>();

		if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
			return ans;
		}

		helper(matrix, 0, matrix.length - 1, 0, matrix[0].length - 1, ans);
		return ans;
	}

	private void helper(int[][] matrix, int r1, int r2, int c1, int c2, List<Integer> ans) {
		if (r1 > r2 || c1 > c2) {
			return;
		}
		// right
		for (int c = c1; c <= c2; c++) {
			ans.add(matrix[r1][c]);
		}

		// down
		for (int r = r1 + 1; r <= r2; r++) {
			ans.add(matrix[r][c2]);
		}

		// if already processed
		if (r1 == r2 || c1 == c2) return;

		// left
		for (int c = c2 - 1; c >= c1; c--) {
			ans.add(matrix[r2][c]);
		}

		// top
		for(int r = r2 - 1; r >= r1 + 1; r--) {
			ans.add(matrix[r][c1]);
		}

		helper(matrix, r1 + 1, r2 - 1, c1 + 1, c2 - 1, ans);
	}
}

Complexity

• ⏰ Time complexity: O(m*n)
• 🧺 Space complexity: O(1)