Problem

You start at the cell (rStart, cStart) of an rows x cols grid facing east. The northwest corner is at the first row and column in the grid, and the southeast corner is at the last row and column.

You will walk in a clockwise spiral shape to visit every position in this grid. Whenever you move outside the grid’s boundary, we continue our walk outside the grid (but may return to the grid boundary later.). Eventually, we reach all rows * cols spaces of the grid.

Return an array of coordinates representing the positions of the grid in the order you visited them.

Examples

Example 1:

1
2

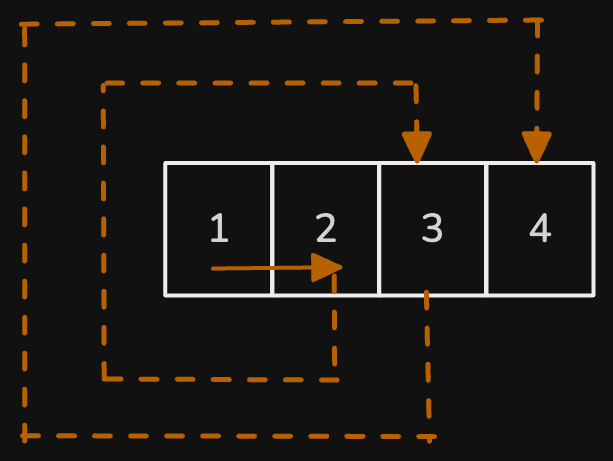
Input: rows = 1, cols = 4, rStart = 0, cStart = 0
Output:[[0,0],[0,1],[0,2],[0,3]]

Example 2:

1
2

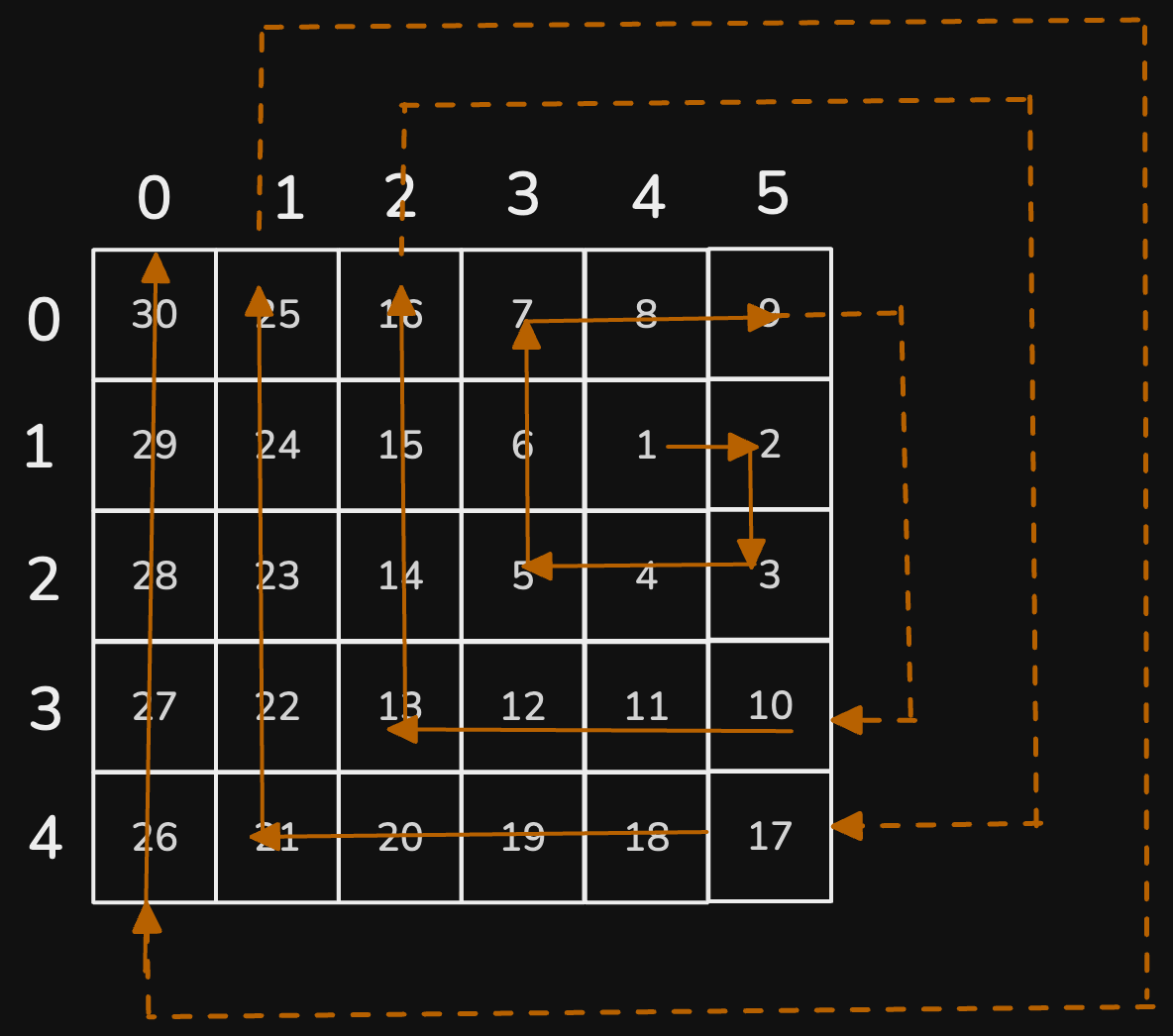
Input: rows = 5, cols = 6, rStart = 1, cStart = 4
Output:[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

Similar Problems

Solution

Method 1 - Simulation

We know that we start from position [rStart, cStart], and we start in direction East, then we go to South, West and north and start the same process.

So, we can define directions:

1
2

// Directions: East, South, West, North
int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

We add [rStart, cStart] to our answer, and go to east.

Then in each direction we take x steps. Initially x = 1, but then it increases by 1 ( - observe carefully - ) when we completed the steps in 2 directions. In eg. 2, we go from 1 → 2, and then 2 → 3, then our number steps increases to 2. Similarly, now we go to 3 → 5, and 5 → 7, then our number of steps increase to 3. So, we go from 7 → out of bounds (right of 9) and so on. So, each time we ran into 2 directions, we have to increase the number of steps. So, we can loop twice for the same number of steps, and increase our steps after that.

Also, when we have walked full x steps, we change the direction as well.

So, now to the code.

Video Explanation

Here is the video explanation for solving the problem:

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public class Solution {
    public int[][] spiralMatrixIII(int rows, int cols, int rStart, int cStart) {
        // Directions: East, South, West, North
        int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        List <int[]> ans = new ArrayList<>();

        // Initial coordinates and direction index
        int r = rStart, c = cStart;
        int directionIdx = 0;
        int steps = 1; // Number of steps to take in current direction
        
        ans.add(new int[] {rStart, cStart}); // Add starting point

        while (ans.size() < rows * cols) {
            for (int i = 0; i < 2; i++) {
                // Looping twice for same number of steps
                for (int j = 0; j < steps; j++) {
                    r += directions[directionIdx][0];
                    c += directions[directionIdx][1];

                    // Check if within bounds
                    if (r >= 0 && r < rows && c >= 0 && c < cols) {
                        ans.add(new int[]{r, c});
                    }
                }
                // Change direction
                directionIdx = (directionIdx + 1) % 4;
            }
            steps++; // Increase the steps after traversing in each direction pair
        }

        return ans.toArray(new int[rows * cols][2]);
    }

}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

def spiralOrder(rows, cols, rStart, cStart):
    # Directions: East, South, West, North
    directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
    result = []
    seen = set()

    # Initial coordinates and direction index
    r, c = rStart, cStart
    direction_idx = 0
    steps = 1  # Number of steps to take in the current direction

    ans.append([rStart, cStart])  # Add starting point
    if rows * cols == 1:
        return ans  # Edge case for single cell

    while len(ans) < rows * cols:
        for _ in range(2):  # Run twice for each pair of directions
            for _ in range(steps):
                r += directions[direction_idx][0]
                c += directions[direction_idx][1]

                # Check if within bounds
                if 0 <= r < rows and 0 <= c < cols:
                    ans.append([r, c])

            # Change direction
            direction_idx = (direction_idx + 1) % 4
        steps += 1  # Increase the steps after traversing in each direction pair

    return ans

Complexity

  • ⏰ Time complexity: O(row * cols)
  • 🧺 Space complexity: O(rows * cols)