Problem

Given the root of a binary search tree (BST) and an integer target, split the tree into two subtrees where the first subtree has nodes that are all smaller or equal to the target value, while the second subtree has all nodes that are greater than the target value. It is not necessarily the case that the tree contains a node with the value target.

Additionally, most of the structure of the original tree should remain. Formally, for any child c with parent p in the original tree, if they are both in the same subtree after the split, then node c should still have the parent p.

Return an array of the two roots of the two subtrees in order.

Examples

Example 1: 

1
2

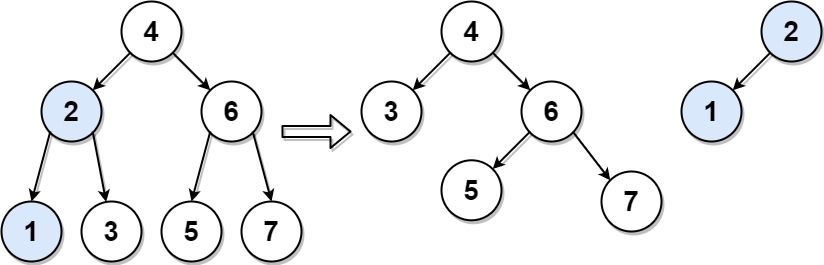
Input: root = [4,2,6,1,3,5,7], target = 2
Output: [[2,1],[4,3,6,null,null,5,7]]

Example 2:

1
2

Input: root = [1], target = 1
Output: [[1],[]]

Constraints:

  • The number of nodes in the tree is in the range [1, 50].
  • 0 <= Node.val, target <= 1000

Solution

Method 1 – Recursive Split

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    public TreeNode[] splitBST(TreeNode root, int target) {
        if (root == null) return new TreeNode[]{null, null};
        if (root.val <= target) {
            TreeNode[] splitted = splitBST(root.right, target);
            root.right = splitted[0];
            return new TreeNode[]{root, splitted[1]};
        } else {
            TreeNode[] splitted = splitBST(root.left, target);
            root.left = splitted[1];
            return new TreeNode[]{splitted[0], root};
        }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution:
    def splitBST(self, root: Optional[TreeNode], target: int) -> list[Optional[TreeNode]]:
        if not root:
            return [None, None]
        if root.val <= target:
            left, right = self.splitBST(root.right, target)
            root.right = left
            return [root, right]
        else:
            left, right = self.splitBST(root.left, target)
            root.left = right
            return [left, root]

Complexity

  • ⏰ Time complexity: O(n) — Each node is visited once.
  • 🧺 Space complexity: O(h) — Due to recursion stack, where h is the tree height.