Problem

You are given two integers height and width representing a garden of size height x width. You are also given:

  • an array tree where tree = [treer, treec] is the position of the tree in the garden,
  • an array squirrel where squirrel = [squirrelr, squirrelc] is the position of the squirrel in the garden,
  • and an array nuts where nuts[i] = [nutir, nutic] is the position of the ith nut in the garden.

The squirrel can only take at most one nut at one time and can move in four directions: up, down, left, and right, to the adjacent cell.

Return theminimal distance for the squirrel to collect all the nuts and put them under the tree one by one.

The distance is the number of moves.

Examples

Example 1:

1
2
3

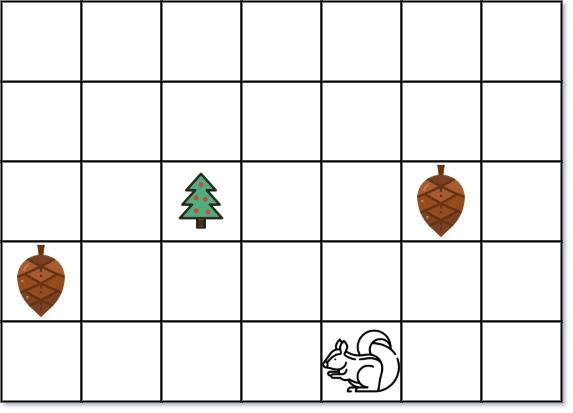
Input: height = 5, width = 7, tree = [2,2], squirrel = [4,4], nuts = [[3,0], [2,5]]
Output: 12
Explanation: The squirrel should go to the nut at [2, 5] first to achieve a minimal distance.

Example 2:

1
2

Input: height = 1, width = 3, tree = [0,1], squirrel = [0,0], nuts = [[0,2]]
Output: 3

Constraints:

  • 1 <= height, width <= 100
  • tree.length == 2
  • squirrel.length == 2
  • 1 <= nuts.length <= 5000
  • nuts[i].length == 2
  • 0 <= treer, squirrelr, nutir <= height
  • 0 <= treec, squirrelc, nutic <= width

Solution

Method 1 – Greedy Calculation of First Nut

Intuition

The squirrel must collect all nuts and bring them to the tree, but it starts at a different position. For all but the first nut, the squirrel must go from the tree to the nut and back. For the first nut, the squirrel starts from its own position. To minimize the total distance, we choose the first nut so that the difference between the squirrel-to-nut and tree-to-nut distances is maximized.

Approach

  1. For each nut, calculate the distance from the tree and from the squirrel.
  2. The total cost is:
    • For all nuts: 2 * distance(tree, nut) (tree to nut and back)
    • For the first nut: replace one tree-to-nut with squirrel-to-nut
    • So, total = sum of 2 * distance(tree, nut) for all nuts, minus the maximum distance(tree, nut) - distance(squirrel, nut)
  3. Return the minimal total distance.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
    public int minDistance(int height, int width, int[] tree, int[] squirrel, int[][] nuts) {
        int total = 0, maxDiff = Integer.MIN_VALUE;
        for (int[] nut : nuts) {
            int treeDist = Math.abs(tree[0] - nut[0]) + Math.abs(tree[1] - nut[1]);
            int squirrelDist = Math.abs(squirrel[0] - nut[0]) + Math.abs(squirrel[1] - nut[1]);
            total += 2 * treeDist;
            maxDiff = Math.max(maxDiff, treeDist - squirrelDist);
        }
        return total - maxDiff;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def minDistance(self, height: int, width: int, tree: list[int], squirrel: list[int], nuts: list[list[int]]) -> int:
        total = 0
        max_diff = float('-inf')
        for nut in nuts:
            tree_dist = abs(tree[0] - nut[0]) + abs(tree[1] - nut[1])
            squirrel_dist = abs(squirrel[0] - nut[0]) + abs(squirrel[1] - nut[1])
            total += 2 * tree_dist
            max_diff = max(max_diff, tree_dist - squirrel_dist)
        return total - max_diff
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int minDistance(int height, int width, vector<int>& tree, vector<int>& squirrel, vector<vector<int>>& nuts) {
        int total = 0, maxDiff = INT_MIN;
        for (const auto& nut : nuts) {
            int treeDist = abs(tree[0] - nut[0]) + abs(tree[1] - nut[1]);
            int squirrelDist = abs(squirrel[0] - nut[0]) + abs(squirrel[1] - nut[1]);
            total += 2 * treeDist;
            maxDiff = max(maxDiff, treeDist - squirrelDist);
        }
        return total - maxDiff;
    }
};

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nuts.
  • 🧺 Space complexity: O(1), only constant extra space is used.