Stamping the Grid

Problem

You are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).

You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements :

1. Cover all the empty cells.
2. Do not cover any of the occupied cells.
3. We can put as many stamps as we want.
4. Stamps can overlap with each other.
5. Stamps are not allowed to be rotated.
6. Stamps must stay completely inside the grid.

Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.

Examples

Example 1

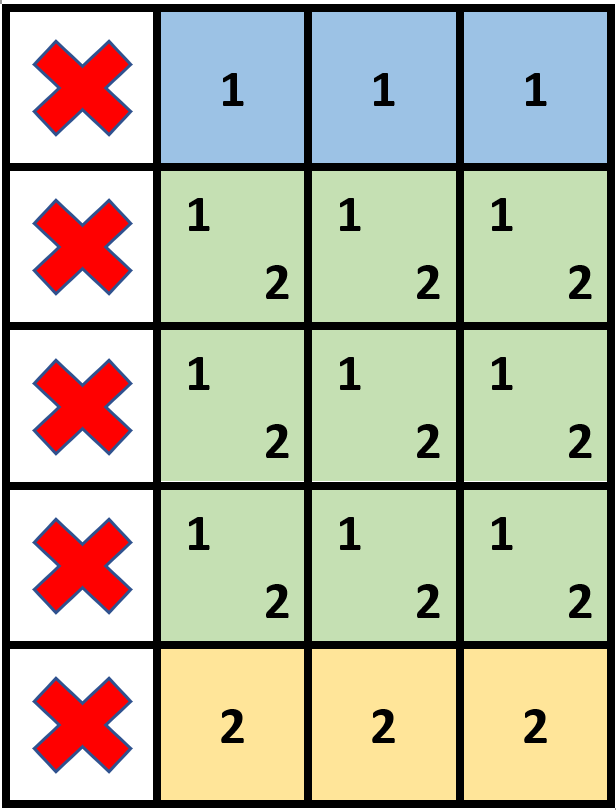
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
Output: true
Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.

Example 2

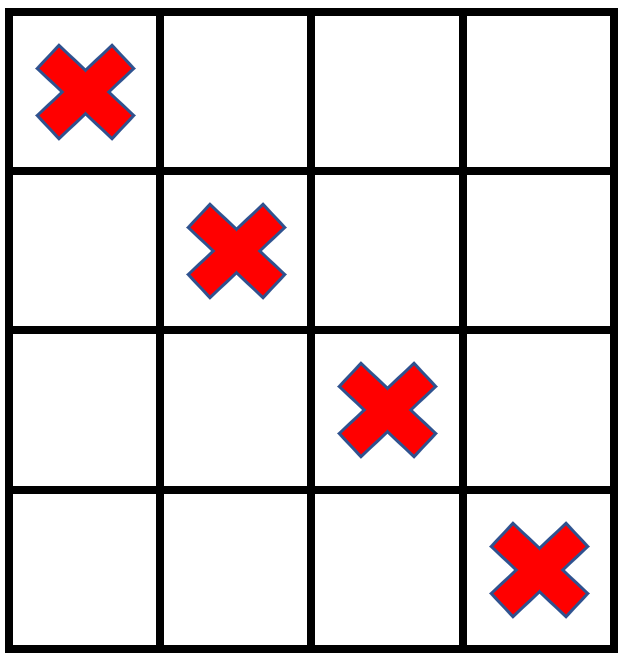
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
Output: false 
Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.

Constraints

• m == grid.length
• n == grid[r].length
• 1 <= m, n <= 10^5
• 1 <= m * n <= 2 * 10^5
• grid[r][c] is either 0 or 1.
• 1 <= stampHeight, stampWidth <= 10^5

Solution

Method 1 – Greedy Coverage with 2D Prefix Sum

Intuition

To efficiently check if all empty cells can be covered by stamps without overlapping occupied cells, we use a 2D prefix sum to quickly verify if a stamp can be placed at any position. We then use another prefix sum to mark all cells covered by at least one stamp and check if every empty cell is covered.

Approach

1. Build a 2D prefix sum of the grid to check if a stamp can be placed at each position (no occupied cells in the stamp area).
2. For each valid stamp position, mark the area covered by the stamp using a difference array.
3. Build a 2D prefix sum of the coverage to check if every empty cell is covered by at least one stamp.
4. Return True if all empty cells are covered, False otherwise.

Code

C++

#include <vector>
using namespace std;
class Solution {
public:
    bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> ps(m+1, vector<int>(n+1));
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                ps[i+1][j+1] = grid[i][j] + ps[i][j+1] + ps[i+1][j] - ps[i][j];
        vector<vector<int>> diff(m+2, vector<int>(n+2));
        for (int i = stampHeight; i <= m; ++i) {
            for (int j = stampWidth; j <= n; ++j) {
                int x1 = i - stampHeight, y1 = j - stampWidth;
                int sum = ps[i][j] - ps[x1][j] - ps[i][y1] + ps[x1][y1];
                if (sum == 0) {
                    diff[x1][y1]++;
                    diff[x1][j]--;
                    diff[i][y1]--;
                    diff[i][j]++;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 0) {
                    int cov = 0;
                    for (int x = 0; x <= i; ++x)
                        for (int y = 0; y <= j; ++y)
                            cov += diff[x][y];
                    if (cov == 0) return false;
                }
            }
        }
        return true;
    }
};

Java

class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m = grid.length, n = grid[0].length;
        int[][] ps = new int[m+1][n+1];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                ps[i+1][j+1] = grid[i][j] + ps[i][j+1] + ps[i+1][j] - ps[i][j];
        int[][] diff = new int[m+2][n+2];
        for (int i = stampHeight; i <= m; ++i) {
            for (int j = stampWidth; j <= n; ++j) {
                int x1 = i - stampHeight, y1 = j - stampWidth;
                int sum = ps[i][j] - ps[x1][j] - ps[i][y1] + ps[x1][y1];
                if (sum == 0) {
                    diff[x1][y1]++;
                    diff[x1][j]--;
                    diff[i][y1]--;
                    diff[i][j]++;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 0) {
                    int cov = 0;
                    for (int x = 0; x <= i; ++x)
                        for (int y = 0; y <= j; ++y)
                            cov += diff[x][y];
                    if (cov == 0) return false;
                }
            }
        }
        return true;
    }
}

Kotlin

class Solution {
    fun possibleToStamp(grid: Array<IntArray>, stampHeight: Int, stampWidth: Int): Boolean {
        val m = grid.size
        val n = grid[0].size
        val ps = Array(m+1) { IntArray(n+1) }
        for (i in 0 until m)
            for (j in 0 until n)
                ps[i+1][j+1] = grid[i][j] + ps[i][j+1] + ps[i+1][j] - ps[i][j]
        val diff = Array(m+2) { IntArray(n+2) }
        for (i in stampHeight..m) {
            for (j in stampWidth..n) {
                val x1 = i - stampHeight
                val y1 = j - stampWidth
                val sum = ps[i][j] - ps[x1][j] - ps[i][y1] + ps[x1][y1]
                if (sum == 0) {
                    diff[x1][y1]++
                    diff[x1][j]--
                    diff[i][y1]--
                    diff[i][j]++
                }
            }
        }
        for (i in 0 until m) {
            for (j in 0 until n) {
                if (grid[i][j] == 0) {
                    var cov = 0
                    for (x in 0..i)
                        for (y in 0..j)
                            cov += diff[x][y]
                    if (cov == 0) return false
                }
            }
        }
        return true
    }
}

Python

class Solution:
    def possibleToStamp(self, grid: list[list[int]], stampHeight: int, stampWidth: int) -> bool:
        m, n = len(grid), len(grid[0])
        ps = [[0]*(n+1) for _ in range(m+1)]
        for i in range(m):
            for j in range(n):
                ps[i+1][j+1] = grid[i][j] + ps[i][j+1] + ps[i+1][j] - ps[i][j]
        diff = [[0]*(n+2) for _ in range(m+2)]
        for i in range(stampHeight, m+1):
            for j in range(stampWidth, n+1):
                x1, y1 = i-stampHeight, j-stampWidth
                s = ps[i][j] - ps[x1][j] - ps[i][y1] + ps[x1][y1]
                if s == 0:
                    diff[x1][y1] += 1
                    diff[x1][j] -= 1
                    diff[i][y1] -= 1
                    diff[i][j] += 1
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 0:
                    cov = 0
                    for x in range(i+1):
                        for y in range(j+1):
                            cov += diff[x][y]
                    if cov == 0:
                        return False
        return True

Rust

impl Solution {
    pub fn possible_to_stamp(grid: Vec<Vec<i32>>, stamp_height: i32, stamp_width: i32) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        let mut ps = vec![vec![0; n+1]; m+1];
        for i in 0..m {
            for j in 0..n {
                ps[i+1][j+1] = grid[i][j] + ps[i][j+1] + ps[i+1][j] - ps[i][j];
            }
        }
        let mut diff = vec![vec![0; n+2]; m+2];
        for i in stamp_height as usize..=m {
            for j in stamp_width as usize..=n {
                let x1 = i - stamp_height as usize;
                let y1 = j - stamp_width as usize;
                let sum = ps[i][j] - ps[x1][j] - ps[i][y1] + ps[x1][y1];
                if sum == 0 {
                    diff[x1][y1] += 1;
                    diff[x1][j] -= 1;
                    diff[i][y1] -= 1;
                    diff[i][j] += 1;
                }
            }
        }
        for i in 0..m {
            for j in 0..n {
                if grid[i][j] == 0 {
                    let mut cov = 0;
                    for x in 0..=i {
                        for y in 0..=j {
                            cov += diff[x][y];
                        }
                    }
                    if cov == 0 {
                        return false;
                    }
                }
            }
        }
        true
    }
}

TypeScript

class Solution {
    possibleToStamp(grid: number[][], stampHeight: number, stampWidth: number): boolean {
        const m = grid.length, n = grid[0].length;
        const ps = Array.from({length: m+1}, () => Array(n+1).fill(0));
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j)
                ps[i+1][j+1] = grid[i][j] + ps[i][j+1] + ps[i+1][j] - ps[i][j];
        const diff = Array.from({length: m+2}, () => Array(n+2).fill(0));
        for (let i = stampHeight; i <= m; ++i) {
            for (let j = stampWidth; j <= n; ++j) {
                const x1 = i - stampHeight, y1 = j - stampWidth;
                const sum = ps[i][j] - ps[x1][j] - ps[i][y1] + ps[x1][y1];
                if (sum === 0) {
                    diff[x1][y1]++;
                    diff[x1][j]--;
                    diff[i][y1]--;
                    diff[i][j]++;
                }
            }
        }
        for (let i = 0; i < m; ++i) {
            for (let j = 0; j < n; ++j) {
                if (grid[i][j] === 0) {
                    let cov = 0;
                    for (let x = 0; x <= i; ++x)
                        for (let y = 0; y <= j; ++y)
                            cov += diff[x][y];
                    if (cov === 0) return false;
                }
            }
        }
        return true;
    }
}

Complexity

• ⏰ Time complexity: O(m * n) – Each cell is processed a constant number of times using prefix sums and difference arrays.
• 🧺 Space complexity: O(m * n) – For prefix sum and difference arrays.