Problem

You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.

Find the shortest path starting from node s and ending at node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:

  • 'L' means to go from a node to its left child node.
  • 'R' means to go from a node to its right child node.
  • 'U' means to go from a node to its parent node.

Return the step-by-step directions of the shortest path from node s to node t.

Examples

Example 1:

1
2
3

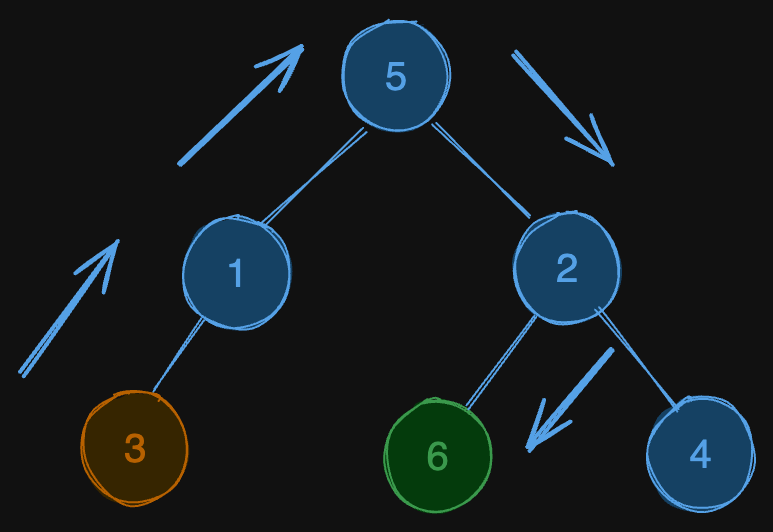
Input: root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output: "UURL"
Explanation: The shortest path is: 3 → 1 → 5 → 2 → 6.

Example 2:

graph TD;
2 --- 1
2 ~~~ N1:::hidden

style 2 fill:#FF9933
style 1 fill:#99FF33
classDef hidden display: none;
  
1
2
3

Input: root = [2,1], startValue = 2, destValue = 1
Output: "L"
Explanation: The shortest path is: 2 → 1.

Solution

To solve this problem, we need to find the shortest path from the node with startValue to the node with destValue in a binary tree. There are multiple ways to do so. One way can be that we use BFS for single source shortest path, but we have to create a binary tree with parent pointer in it, to store the relationships.

But another way can be we use the binary tree data structure and find LCA.

Method 1 - LCA

The main steps to achieve this are:

  1. Find the Node with the Given Values: We need to locate the nodes corresponding to startValue and destValue.
  2. Determine the Lowest Common Ancestor (LCA): The LCA of the start and destination nodes helps in determining the shortest path between them. We have already seen Lowest Common Ancestor of a Binary Tree here.
  3. Construct Paths from LCA to Start and Destination Nodes: Using Depth First Search (DFS), construct the paths from the LCA to both the start and destination nodes.
  4. Combine the Paths: Transform the path from start to LCA into ‘U’s and concatenate with the path from LCA to destination.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

public class Solution {

	public String getDirections(TreeNode root, int startValue, int destValue) {
		// Step 1: Find the LCA of startValue and destValue
		TreeNode lca = findLCA(root, startValue, destValue);

		// Step 2: Find the path from LCA to startValue
		StringBuilder pathToStart = new StringBuilder();
		findPath(lca, startValue, pathToStart);

		// Step 3: Find the path from LCA to destValue
		StringBuilder pathToDest = new StringBuilder();
		findPath(lca, destValue, pathToDest);

		// Step 4: Convert pathToStart to all 'U's and combine paths
		for (int i = 0; i < pathToStart.length(); i++) {
			pathToStart.setCharAt(i, 'U');
		}

		// Combine paths
		return pathToStart.toString() + pathToDest.toString();
	}


	private TreeNode findLCA(TreeNode root, int p, int q) {
		if (root == null || root.val == p || root.val == q) {
			return root;
		}

		TreeNode left = findLCA(root.left, p, q);
		TreeNode right = findLCA(root.right, p, q);

		if (left != null && right != null) {
			return root;
		}

		return left != null ? left : right;
	}


	private boolean findPath(TreeNode root, int value, StringBuilder path) {
		if (root == null) {
			return false;
		}

		if (root.val == value) {
			return true;
		}

		path.append('L');

		if (findPath(root.left, value, path)) {
			return true;
		}

		path.deleteCharAt(path.length() - 1);
		path.append('R');

		if (findPath(root.right, value, path)) {
			return true;
		}

		path.deleteCharAt(path.length() - 1);
		return false;
	}
}

Complexity

  • ⏰ Time complexity: O(n) where n is number of nodes in tree. - Each tree traversal for findLCA and findPath is O(n).
  • 🧺 Space complexity: O(h) where h is height of tree, and that comes from recursion stack. Space for the path strings will be O(h) as well.

Dry Run

Lets dry run with eg. 1 - root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6 findLCA(root, 3,6) finds node with value 5.

Now, finding path from 5 to 3 is LL, and finding path from 5 to 6 returns RL.

Now, we convert LL to UU, and concatenate RL. Our path becomes UURL.