problemhardalgorithmsleetcode-1591leetcode 1591leetcode1591

Strange Printer II

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There is a strange printer with the following two special requirements:

  • On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
  • Once the printer has used a color for the above operation, the same color cannot be used again.

You are given a m x n matrix targetGrid, where targetGrid[row][col] is the color in the position (row, col) of the grid.

Return true if it is possible to print the matrixtargetGrid _,_otherwise, returnfalse.

Examples

Example 1


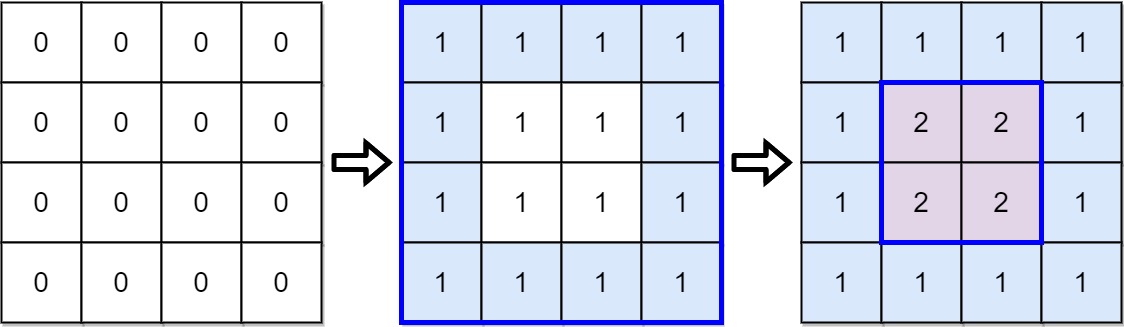
![](https://assets.leetcode.com/uploads/2021/12/23/print1.jpg)

Input: targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
Output: true

Example 2


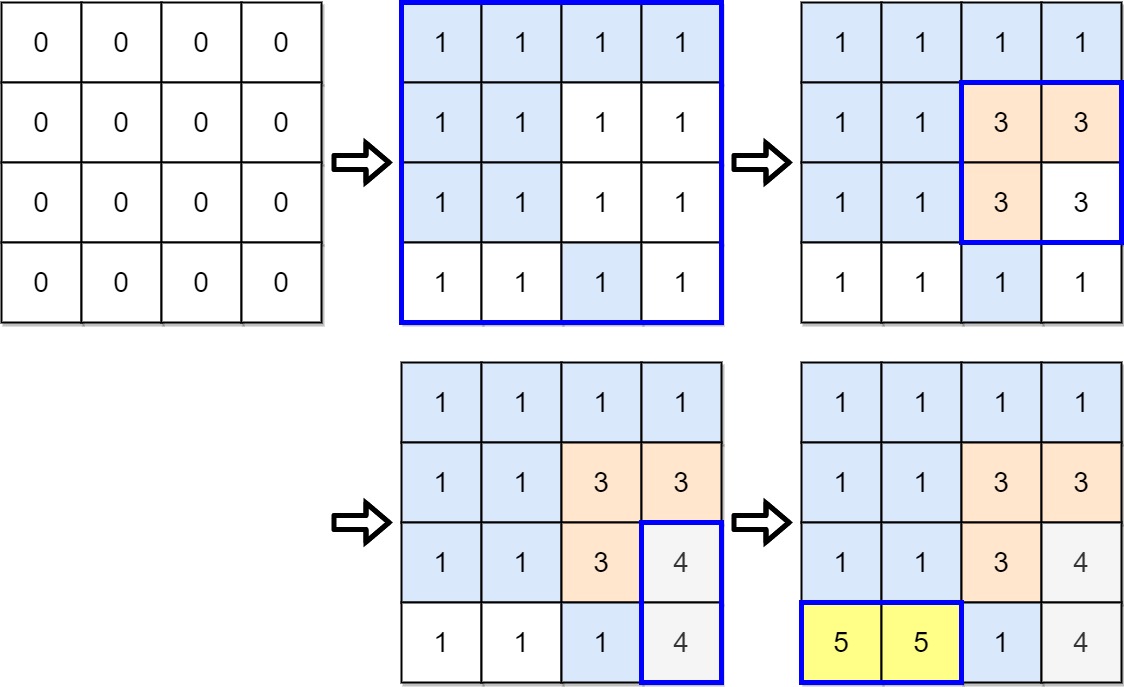
![](https://assets.leetcode.com/uploads/2021/12/23/print2.jpg)

Input: targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
Output: true

Example 3

Input: targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
Output: false
Explanation: It is impossible to form targetGrid because it is not allowed to print the same color in different turns.

Constraints

  • m == targetGrid.length
  • n == targetGrid[i].length
  • 1 <= m, n <= 60
  • 1 <= targetGrid[row][col] <= 60

Solution

Method 1 - Topological Sort on Color Dependencies

Intuition

For each color, find its minimal bounding rectangle. If any other color appears inside this rectangle, that color must be printed before the current color. This forms a dependency graph. If the dependency graph is acyclic (can be topologically sorted), the answer is true; otherwise, false.

Approach

  1. For each color, compute its bounding rectangle (min/max row/col).
  2. For each color, check all cells in its rectangle. If another color is found, add a dependency edge.
  3. Perform topological sort on the dependency graph. If possible, return true; else, false.

Code

C++
#include <vector>
#include <queue>
using namespace std;
bool isPrintable(vector<vector<int>>& grid) {
    int m = grid.size(), n = grid[0].size();
    vector<int> minr(61, m), maxr(61, -1), minc(61, n), maxc(61, -1);
    for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) {
        int c = grid[i][j];
        minr[c] = min(minr[c], i); maxr[c] = max(maxr[c], i);
        minc[c] = min(minc[c], j); maxc[c] = max(maxc[c], j);
    }
    vector<vector<int>> g(61);
    vector<int> indeg(61);
    for (int c = 1; c <= 60; ++c) if (maxr[c] != -1) {
        for (int i = minr[c]; i <= maxr[c]; ++i)
            for (int j = minc[c]; j <= maxc[c]; ++j)
                if (grid[i][j] != c) {
                    g[c].push_back(grid[i][j]);
                    indeg[grid[i][j]]++;
                }
    }
    queue<int> q;
    for (int c = 1; c <= 60; ++c) if (maxr[c] != -1 && indeg[c] == 0) q.push(c);
    int cnt = 0;
    while (!q.empty()) {
        int c = q.front(); q.pop(); cnt++;
        for (int nei : g[c]) if (--indeg[nei] == 0) q.push(nei);
    }
    int total = 0;
    for (int c = 1; c <= 60; ++c) if (maxr[c] != -1) total++;
    return cnt == total;
}
Go
func isPrintable(grid [][]int) bool {
    m, n := len(grid), len(grid[0])
    minr, maxr := make([]int, 61), make([]int, 61)
    minc, maxc := make([]int, 61), make([]int, 61)
    for i := range minr { minr[i] = m; maxr[i] = -1; minc[i] = n; maxc[i] = -1 }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            c := grid[i][j]
            if i < minr[c] { minr[c] = i }
            if i > maxr[c] { maxr[c] = i }
            if j < minc[c] { minc[c] = j }
            if j > maxc[c] { maxc[c] = j }
        }
    }
    g := make([][]int, 61)
    indeg := make([]int, 61)
    for c := 1; c <= 60; c++ {
        if maxr[c] == -1 { continue }
        for i := minr[c]; i <= maxr[c]; i++ {
            for j := minc[c]; j <= maxc[c]; j++ {
                if grid[i][j] != c {
                    g[c] = append(g[c], grid[i][j])
                    indeg[grid[i][j]]++
                }
            }
        }
    }
    q := []int{}
    for c := 1; c <= 60; c++ {
        if maxr[c] != -1 && indeg[c] == 0 {
            q = append(q, c)
        }
    }
    cnt, total := 0, 0
    for c := 1; c <= 60; c++ { if maxr[c] != -1 { total++ } }
    for len(q) > 0 {
        c := q[0]; q = q[1:]; cnt++
        for _, nei := range g[c] {
            indeg[nei]--
            if indeg[nei] == 0 { q = append(q, nei) }
        }
    }
    return cnt == total
}
Java
import java.util.*;
class Solution {
    public boolean isPrintable(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[] minr = new int[61], maxr = new int[61], minc = new int[61], maxc = new int[61];
        Arrays.fill(minr, m); Arrays.fill(maxr, -1); Arrays.fill(minc, n); Arrays.fill(maxc, -1);
        for (int i = 0; i < m; i++) for (int j = 0; j < n; j++) {
            int c = grid[i][j];
            minr[c] = Math.min(minr[c], i); maxr[c] = Math.max(maxr[c], i);
            minc[c] = Math.min(minc[c], j); maxc[c] = Math.max(maxc[c], j);
        }
        List<Integer>[] g = new List[61];
        for (int i = 0; i < 61; i++) g[i] = new ArrayList<>();
        int[] indeg = new int[61];
        for (int c = 1; c <= 60; c++) if (maxr[c] != -1) {
            for (int i = minr[c]; i <= maxr[c]; i++)
                for (int j = minc[c]; j <= maxc[c]; j++)
                    if (grid[i][j] != c) {
                        g[c].add(grid[i][j]);
                        indeg[grid[i][j]]++;
                    }
        }
        Queue<Integer> q = new ArrayDeque<>();
        for (int c = 1; c <= 60; c++) if (maxr[c] != -1 && indeg[c] == 0) q.add(c);
        int cnt = 0, total = 0;
        for (int c = 1; c <= 60; c++) if (maxr[c] != -1) total++;
        while (!q.isEmpty()) {
            int c = q.poll(); cnt++;
            for (int nei : g[c]) if (--indeg[nei] == 0) q.add(nei);
        }
        return cnt == total;
    }
}
Kotlin
fun isPrintable(grid: Array<IntArray>): Boolean {
    val m = grid.size; val n = grid[0].size
    val minr = IntArray(61) { m }; val maxr = IntArray(61) { -1 }
    val minc = IntArray(61) { n }; val maxc = IntArray(61) { -1 }
    for (i in 0 until m) for (j in 0 until n) {
        val c = grid[i][j]
        minr[c] = minOf(minr[c], i); maxr[c] = maxOf(maxr[c], i)
        minc[c] = minOf(minc[c], j); maxc[c] = maxOf(maxc[c], j)
    }
    val g = Array(61) { mutableListOf<Int>() }
    val indeg = IntArray(61)
    for (c in 1..60) if (maxr[c] != -1) {
        for (i in minr[c]..maxr[c]) for (j in minc[c]..maxc[c])
            if (grid[i][j] != c) {
                g[c].add(grid[i][j])
                indeg[grid[i][j]]++
            }
    }
    val q = ArrayDeque<Int>()
    for (c in 1..60) if (maxr[c] != -1 && indeg[c] == 0) q.add(c)
    var cnt = 0; var total = 0
    for (c in 1..60) if (maxr[c] != -1) total++
    while (q.isNotEmpty()) {
        val c = q.removeFirst(); cnt++
        for (nei in g[c]) if (--indeg[nei] == 0) q.add(nei)
    }
    return cnt == total
}
Python
def isPrintable(targetGrid: list[list[int]]) -> bool:
    m, n = len(targetGrid), len(targetGrid[0])
    minr = [m]*61; maxr = [-1]*61; minc = [n]*61; maxc = [-1]*61
    for i in range(m):
        for j in range(n):
            c = targetGrid[i][j]
            minr[c] = min(minr[c], i); maxr[c] = max(maxr[c], i)
            minc[c] = min(minc[c], j); maxc[c] = max(maxc[c], j)
    g = [[] for _ in range(61)]
    indeg = [0]*61
    for c in range(1, 61):
        if maxr[c] == -1: continue
        for i in range(minr[c], maxr[c]+1):
            for j in range(minc[c], maxc[c]+1):
                if targetGrid[i][j] != c:
                    g[c].append(targetGrid[i][j])
                    indeg[targetGrid[i][j]] += 1
    q = [c for c in range(1, 61) if maxr[c] != -1 and indeg[c] == 0]
    cnt = 0; total = sum(1 for c in range(1, 61) if maxr[c] != -1)
    while q:
        c = q.pop(0); cnt += 1
        for nei in g[c]:
            indeg[nei] -= 1
            if indeg[nei] == 0:
                q.append(nei)
    return cnt == total
Rust
pub fn is_printable(target_grid: Vec<Vec<i32>>) -> bool {
    let m = target_grid.len();
    let n = target_grid[0].len();
    let mut minr = vec![m as i32; 61];
    let mut maxr = vec![-1; 61];
    let mut minc = vec![n as i32; 61];
    let mut maxc = vec![-1; 61];
    for i in 0..m {
        for j in 0..n {
            let c = target_grid[i][j] as usize;
            minr[c] = minr[c].min(i as i32);
            maxr[c] = maxr[c].max(i as i32);
            minc[c] = minc[c].min(j as i32);
            maxc[c] = maxc[c].max(j as i32);
        }
    }
    let mut g = vec![vec![]; 61];
    let mut indeg = vec![0; 61];
    for c in 1..=60 {
        if maxr[c] == -1 { continue; }
        for i in minr[c]..=maxr[c] {
            for j in minc[c]..=maxc[c] {
                let cc = target_grid[i as usize][j as usize] as usize;
                if cc != c {
                    g[c].push(cc);
                    indeg[cc] += 1;
                }
            }
        }
    }
    let mut q = vec![];
    for c in 1..=60 {
        if maxr[c] != -1 && indeg[c] == 0 {
            q.push(c);
        }
    }
    let mut cnt = 0;
    let total = (1..=60).filter(|&c| maxr[c] != -1).count();
    while let Some(c) = q.pop() {
        cnt += 1;
        for &nei in &g[c] {
            indeg[nei] -= 1;
            if indeg[nei] == 0 {
                q.push(nei);
            }
        }
    }
    cnt == total
}
TypeScript
function isPrintable(targetGrid: number[][]): boolean {
    const m = targetGrid.length, n = targetGrid[0].length;
    const minr = Array(61).fill(m), maxr = Array(61).fill(-1);
    const minc = Array(61).fill(n), maxc = Array(61).fill(-1);
    for (let i = 0; i < m; i++) for (let j = 0; j < n; j++) {
        const c = targetGrid[i][j];
        minr[c] = Math.min(minr[c], i); maxr[c] = Math.max(maxr[c], i);
        minc[c] = Math.min(minc[c], j); maxc[c] = Math.max(maxc[c], j);
    }
    const g: number[][] = Array.from({length: 61}, () => []);
    const indeg = Array(61).fill(0);
    for (let c = 1; c <= 60; c++) if (maxr[c] !== -1) {
        for (let i = minr[c]; i <= maxr[c]; i++)
            for (let j = minc[c]; j <= maxc[c]; j++)
                if (targetGrid[i][j] !== c) {
                    g[c].push(targetGrid[i][j]);
                    indeg[targetGrid[i][j]]++;
                }
    }
    let q: number[] = [];
    for (let c = 1; c <= 60; c++) if (maxr[c] !== -1 && indeg[c] === 0) q.push(c);
    let cnt = 0, total = 0;
    for (let c = 1; c <= 60; c++) if (maxr[c] !== -1) total++;
    while (q.length) {
        const c = q.shift()!; cnt++;
        for (const nei of g[c]) if (--indeg[nei] === 0) q.push(nei);
    }
    return cnt === total;
}

Complexity

  • ⏰ Time complexity: O(m * n * C) where C is the number of colors (≤ 60).
  • 🧺 Space complexity: O(C^2) for the dependency graph.

Comments