Problem

Definitions

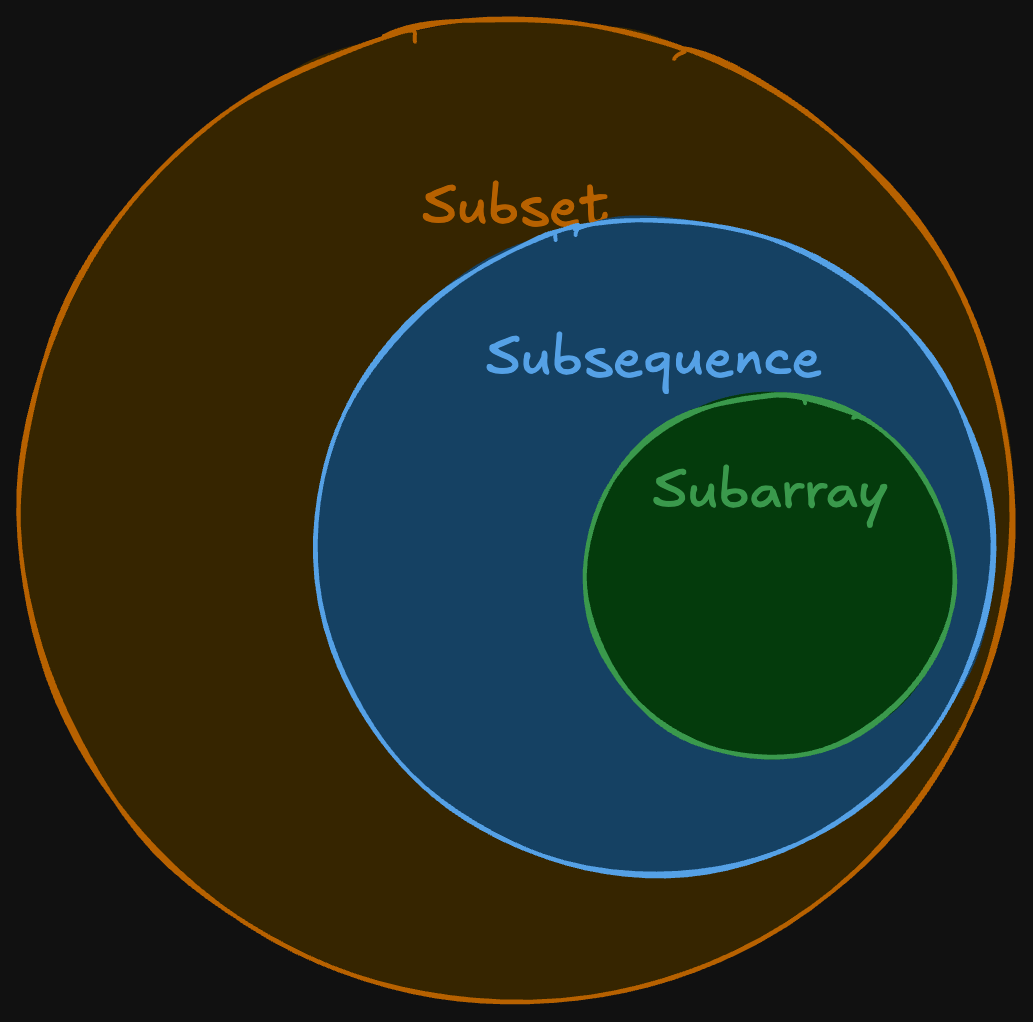
  • A subarray is a contiguous part of array and maintains relative ordering of elements. For an array/string of size n, there are n*(n+1)/2 non-empty subarrays/substrings.

  • A subsequence maintain relative ordering of elements but may or may not be a contiguous part of an array. For a sequence of size n, we can have 2^n-1 non-empty sub-sequences in total.

  • A subset MAY NOT maintain relative ordering of elements and can or cannot be a contiguous part of an array. For a set of size n, we can have (2^n) sub-sets in total.

Some interesting observations :

  • Every Subarray is a Subsequence.
  • Every Subsequence is a Subset.

Here is a short video on it:

Video explanation

Here is the video explaining this method in detail. Please check it out:

Examples

Consider the array [1, 2, 3, 4]:

  • Subarray: [1, 2], [1, 2, 3] (continuous and ordered)
  • Subsequence: [1, 2, 4] (not continuous but ordered)
  • Subset: [1, 3, 2] (not continuous and not ordered)