Problem

You are given an undirected tree rooted at node 0, with n nodes numbered from 0 to n - 1. The tree is represented by a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates an edge between nodes ui and vi.

You are also given an integer array nums of length n, where nums[i] represents the value at node i, and an integer k.

You may perform inversion operations on a subset of nodes subject to the following rules:

  • Subtree Inversion Operation:

    • When you invert a node, every value in the subtree rooted at that node is multiplied by -1.

  • Distance Constraint on Inversions:

    • You may only invert a node if it is “sufficiently far” from any other inverted node.
    • Specifically, if you invert two nodes a and b such that one is an ancestor of the other (i.e., if LCA(a, b) = a or LCA(a, b) = b), then the distance (the number of edges on the unique path between them) must be at least k.

Return the maximum possible sum of the tree’s node values after applying inversion operations.

Examples

Example 1

1
2
3

Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], nums =
[4,-8,-6,3,7,-2,5], k = 2
Output: 27

Explanation:

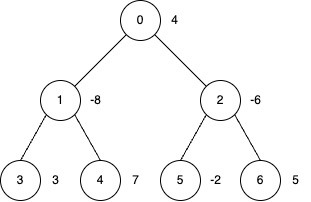
  • Apply inversion operations at nodes 0, 3, 4 and 6.
  • The final nums array is [-4, 8, 6, 3, 7, 2, 5], and the total sum is 27.

Example 2

1
2

Input: edges = [[0,1],[1,2],[2,3],[3,4]], nums = [-1,3,-2,4,-5], k = 2
Output: 9

Explanation:

  • Apply the inversion operation at node 4.
  • The final nums array becomes [-1, 3, -2, 4, 5], and the total sum is 9.

Example 3

1
2
3
4

Input: edges = [[0,1],[0,2]], nums = [0,-1,-2], k = 3
Output: 3
Explanation:
Apply inversion operations at nodes 1 and 2.

Constraints

  • 2 <= n <= 5 * 10^4
  • edges.length == n - 1
  • edges[i] = [ui, vi]
  • 0 <= ui, vi < n
  • nums.length == n
  • -5 * 10^4 <= nums[i] <= 5 * 10^4
  • 1 <= k <= 50
  • The input is generated such that edges represents a valid tree.

Solution

Method 1 – DFS with Bitmask Dynamic Programming

Intuition

We need to maximize the sum of the nums array after performing at most k subtree inversions. Each inversion flips the sign of all values in a subtree. The optimal solution involves choosing up to k subtrees such that their inversions do not overlap and the total sum is maximized. We use DFS to compute subtree sums and DP with bitmasking to track inversion choices efficiently.

Approach

  1. Build the tree from the edges.
  2. Use DFS to compute the sum of each subtree and store the children for each node.
  3. Use DP with memoization: dp[node][inversions_left] gives the max sum for the subtree rooted at node with a given number of inversions left.
  4. For each node, try all possible ways to distribute inversions among its children and itself.
  5. If we invert the current node’s subtree, subtract twice its sum from the total.
  6. Return the maximum sum after at most k inversions.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include <vector>
#include <unordered_map>
using namespace std;
class Solution {
public:
    int subtreeInversionSum(vector<vector<int>>& edges, vector<int>& nums, int k) {
        int n = nums.size();
        vector<vector<int>> tree(n);
        for (auto& e : edges) {
            tree[e[0]].push_back(e[1]);
            tree[e[1]].push_back(e[0]);
        }
        vector<int> subsum(n);
        function<void(int,int)> dfs = [&](int u, int p) {
            subsum[u] = nums[u];
            for (int v : tree[u]) {
                if (v == p) continue;
                dfs(v, u);
                subsum[u] += subsum[v];
            }
        };
        dfs(0, -1);
        vector<vector<int>> dp(n, vector<int>(k+1, INT_MIN));
        function<int(int,int,int)> solve = [&](int u, int p, int rem) {
            if (dp[u][rem] != INT_MIN) return dp[u][rem];
            int res = subsum[u];
            for (int take = 1; take <= rem; ++take) {
                int cur = -subsum[u];
                for (int v : tree[u]) {
                    if (v == p) continue;
                    cur += solve(v, u, take-1);
                }
                res = max(res, cur);
            }
            for (int v : tree[u]) {
                if (v == p) continue;
                for (int t = 0; t <= rem; ++t) {
                    res = max(res, subsum[u] - subsum[v] + solve(v, u, t));
                }
            }
            return dp[u][rem] = res;
        };
        return solve(0, -1, k);
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

import java.util.*;
class Solution {
    public int subtreeInversionSum(int[][] edges, int[] nums, int k) {
        int n = nums.length;
        List<List<Integer>> tree = new ArrayList<>();
        for (int i = 0; i < n; ++i) tree.add(new ArrayList<>());
        for (int[] e : edges) {
            tree.get(e[0]).add(e[1]);
            tree.get(e[1]).add(e[0]);
        }
        int[] subsum = new int[n];
        dfs(0, -1, tree, nums, subsum);
        int[][] dp = new int[n][k+1];
        for (int[] d : dp) Arrays.fill(d, Integer.MIN_VALUE);
        return solve(0, -1, k, tree, subsum, dp);
    }
    private void dfs(int u, int p, List<List<Integer>> tree, int[] nums, int[] subsum) {
        subsum[u] = nums[u];
        for (int v : tree.get(u)) {
            if (v == p) continue;
            dfs(v, u, tree, nums, subsum);
            subsum[u] += subsum[v];
        }
    }
    private int solve(int u, int p, int rem, List<List<Integer>> tree, int[] subsum, int[][] dp) {
        if (dp[u][rem] != Integer.MIN_VALUE) return dp[u][rem];
        int res = subsum[u];
        for (int take = 1; take <= rem; ++take) {
            int cur = -subsum[u];
            for (int v : tree.get(u)) {
                if (v == p) continue;
                cur += solve(v, u, take-1, tree, subsum, dp);
            }
            res = Math.max(res, cur);
        }
        for (int v : tree.get(u)) {
            if (v == p) continue;
            for (int t = 0; t <= rem; ++t) {
                res = Math.max(res, subsum[u] - subsum[v] + solve(v, u, t, tree, subsum, dp));
            }
        }
        return dp[u][rem] = res;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution:
    def subtreeInversionSum(self, edges: list[list[int]], nums: list[int], k: int) -> int:
        from collections import defaultdict
        n = len(nums)
        tree = defaultdict(list)
        for u, v in edges:
            tree[u].append(v)
            tree[v].append(u)
        subsum = [0] * n
        def dfs(u: int, p: int) -> int:
            subsum[u] = nums[u]
            for v in tree[u]:
                if v == p: continue
                subsum[u] += dfs(v, u)
            return subsum[u]
        dfs(0, -1)
        from functools import lru_cache
        @lru_cache(None)
        def solve(u: int, p: int, rem: int) -> int:
            res = subsum[u]
            for take in range(1, rem+1):
                cur = -subsum[u]
                for v in tree[u]:
                    if v == p: continue
                    cur += solve(v, u, take-1)
                res = max(res, cur)
            for v in tree[u]:
                if v == p: continue
                for t in range(rem+1):
                    res = max(res, subsum[u] - subsum[v] + solve(v, u, t))
            return res
        return solve(0, -1, k)

Complexity

  • ⏰ Time complexity: O(n * k^2) – Each node and inversion count is considered, with DP and DFS.
  • 🧺 Space complexity: O(n * k) – For DP table and subtree sums.