Sum of All Subset XOR Totals

Problem

The XOR total of an array is defined as the bitwise XOR of all its elements, or 0 if the array is empty.

For example, the XOR total of the array [2,5,6] is 2 XOR 5 XOR 6 = 1.

Given an array nums, return the sum of all XOR totals for every subset of nums.

Note: Subsets with the same elements should be counted multiple times.

An array a is a subset of an array b if a can be obtained from b by deleting some (possibly zero) elements of b.

Examples

Example 1:

Input: nums = [1,3]
Output: 6
Explanation: The 4 subsets of [1,3] are:
- The empty subset has an XOR total of 0.
- [1] has an XOR total of 1.
- [3] has an XOR total of 3.
- [1,3] has an XOR total of 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6

Example 2:

Input: nums = [5,1,6]
Output: 28
Explanation: The 8 subsets of [5,1,6] are:
- The empty subset has an XOR total of 0.
- [5] has an XOR total of 5.
- [1] has an XOR total of 1.
- [6] has an XOR total of 6.
- [5,1] has an XOR total of 5 XOR 1 = 4.
- [5,6] has an XOR total of 5 XOR 6 = 3.
- [1,6] has an XOR total of 1 XOR 6 = 7.
- [5,1,6] has an XOR total of 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

Example 3:

Input: nums = [3,4,5,6,7,8]
Output: 480
Explanation: The sum of all XOR totals for every subset is 480.

Solution

Method 1 - Using backtracking

This problem is very similar to [subsets problem](subsets-1), where we generate subset of all elements in array, just that we xor the elements. We may exclude or include the element when we are doing dfs on nums:

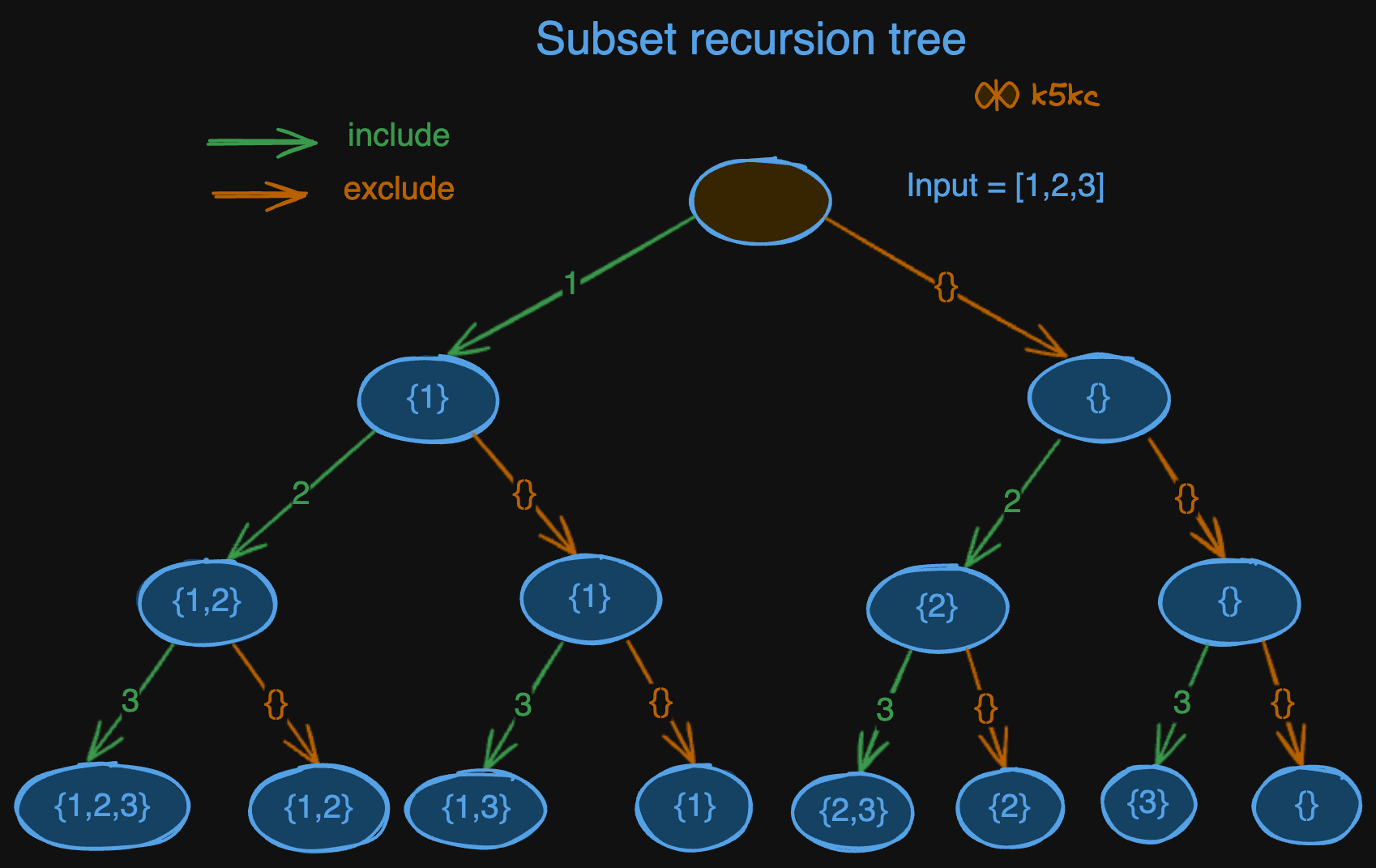
Approach

At each step, decide whether to include or exclude the current element in the subset.
Use recursive calls to compute the XOR totals for both possibilities:
- Include the current number (take XOR).
- Skip the current number (ignore XOR).
For every subset explored, accumulate the XOR total into a running sum.
Base case handles when we've reached the end of the array.

Video explanation

Here is the video explaining this method in detail. Please check it out:

Code

Java

class Solution {
	public int subsetXORSum(int[] nums) {
		return dfs(nums, 0, 0);
	}
	
	private int dfs(int[] nums, int idx, int currentXor) {
		if (idx >= nums.length) {
			return currentXor;
		}
		
		int withElement = dfs(nums, idx + 1, currentXor ^ nums[idx]);
		
		int withoutElement = dfs(nums, idx + 1, currentXor);
		
		return withElement + withoutElement;
	}
}

Python

class Solution:
    def subsetXORSum(self, nums):
        def dfs(idx, current_xor):
            if idx >= len(nums):
                return current_xor
            
            # Include the current element in the subset
            with_element = dfs(idx + 1, current_xor ^ nums[idx])
            
            # Exclude the current element from the subset
            without_element = dfs(idx + 1, current_xor)
            
            # Return the sum of XOR totals from both subsets
            return with_element + without_element
        
        return dfs(0, 0)

Complexity

⏰ Time complexity: O(2^n). For an array of size n, there are (2^n) subsets. This is because each element in the array has two choices: to be included in the subset or not.
- Each recursive call processes one subset, and there are (2^n) recursive calls in total.
🧺 Space complexity: O(n). The recursion goes as deep as the length of the array nums. Each recursive call adds a frame to the call stack.