Problem

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

Examples

Example 1:

graph TD;
0 --- 1 & 2
2 --- 3 & 4 & 5
  
1
2
3
4
5
6
7
8

Input:
n = 6, edges =[[0,1],[0,2],[2,3],[2,4],[2,5]]
Output:
 [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

graph TD;
0
  
1
2
3
4

Input:
n = 1, edges = []
Output:
 [0]

Example 3:

graph TD;
0 --- 1
  
1
2
3
4

Input:
n = 2, edges =[[1,0]]
Output:
 [1,1]

Solution

Method 1 - Pre-order and Post-order Traversal

Solve for root

Lets start with example 1, and lets say we have to find the sum of distances only for root node.

graph TD;
0 --- 1 & 2
2 --- 3 & 4 & 5

style 0 fill:#f9f

Then, we can see following:

1
2
3

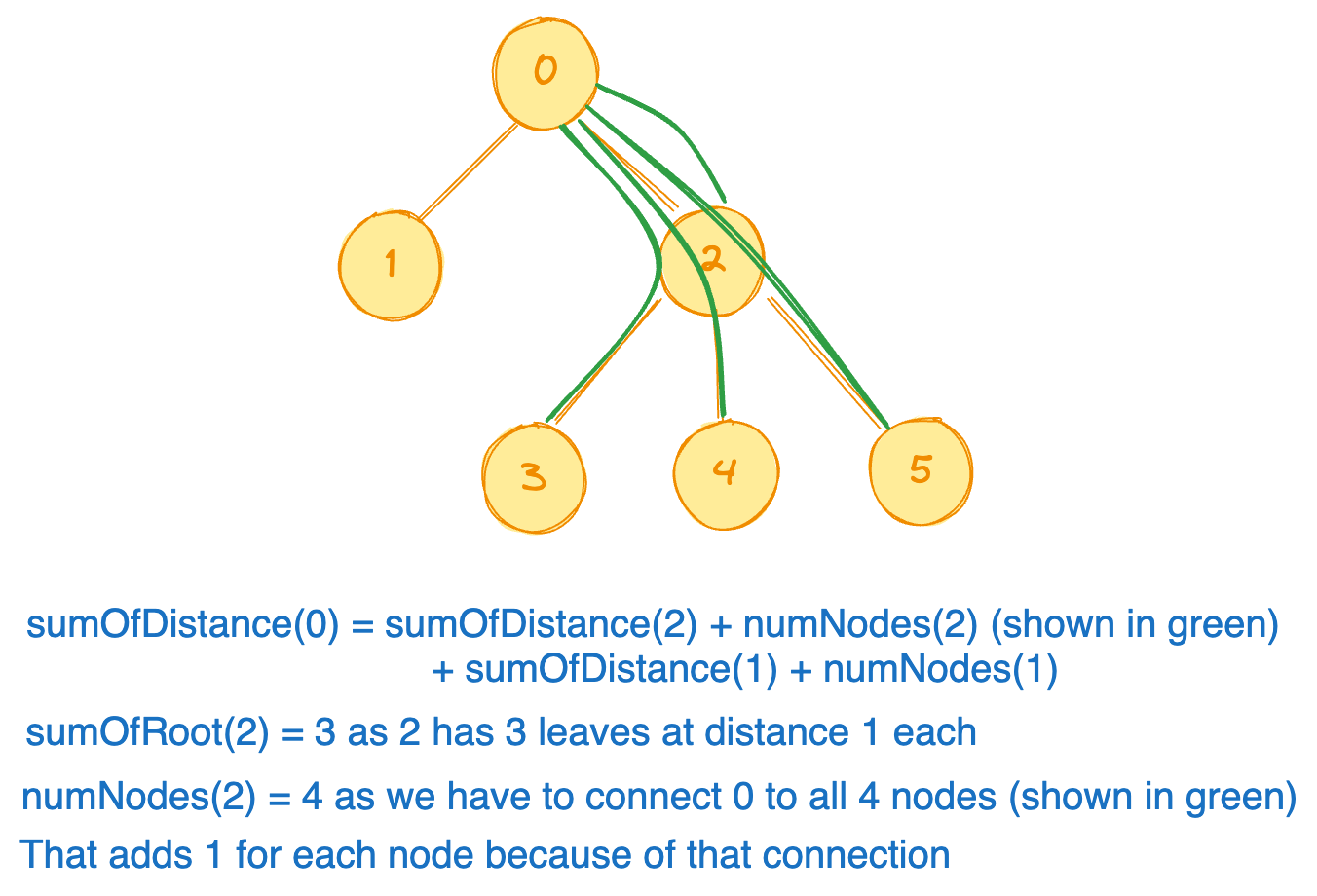
sumOfDistance(0) = sumOfDistance(1) + number of nodes in subtree with root 1 +
				   sumOfDistance(2) + number of nodes in subtree with root 2
sumOfDistance(0) = 0 + 1 + 3 + 4 = 8

sumOfDistance(1) means distance, when 1 is root (see tree below), and it is 0 because it doesn’t have any child.

graph TD;
1

style 1 fill:#f9f

sumOfDistance(2) is 3, because we can see it has 3 children, all as leaf (see below)

graph TD;
2 --- 3 & 4 & 5

style 2 fill:#f9f

We are adding the number of nodes of subtree because every node in subtree will be 1 unit more far from the original root.

For eg. for subtree with 2 as root, distance from 0 adds 4:

We need two arrays cnt and ans. cnt will store the number of nodes in each subtree and ans will the store the answer as discussed above. Below is the code.

Original Solution

We can run the dfs function above for every node and get the solution. This will result in O(N * N) time complexity. We can do this in O(N) time using a technique popularly known as re-rooting technique.

Suppose, instead of 0 as root, we take 2 as root. What changes will we observe?

graph TD;
2 --- 0 & 3 & 4 & 5
0 --- 1

style 2 fill:#f9f

cnt[2] nodes got closer by 1 unit to new root, and n - cnt[2] nodes got farther by 1 unit from new root.

1

ans[2] = ans[0] - cnt[2] + n - cnt[2]

i.e.

1

ans[newRoot] = ans[oldRoot] - cnt[newRoot] + n - cnt[newRoot];

Refer to dfs2 function for that.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class Solution {
    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        List<Integer>[] tree = buildGraph(n, edges);

        int[] cnt = new int[n];
        int[] ans = new int[n];

        dfs(tree, 0, -1, cnt, ans);
        dfs2(tree, 0, -1, cnt, ans);

        return ans;
    }

    private List<Integer>[] buildGraph(int n, int[][] edges) {
        List<Integer>[] tree = new List[n];

        for (int i = 0; i < n; i++) {
            tree[i] = new ArrayList<>();
        }

        for (int[] edge : edges) {
            tree[edge[0]].add(edge[1]);
            tree[edge[1]].add(edge[0]);
        }
        return tree;
    }

    private void dfs(List<Integer>[] tree, int cur, int pre, int[] cnt, int[] ans) {
        for (int child : tree[cur]) {
            if (child != pre) {
                dfs(tree, child, cur, cnt, ans);
                ans[cur] += ans[child] + cnt[child];
                cnt[cur] += cnt[child];
            }
        }
        cnt[cur]++;
    }

    private void dfs2(List<Integer>[] tree, int cur, int pre, int[] cnt, int[] ans) {
        for (int child : tree[cur]) {
            if (child != pre) {
                ans[child] = ans[cur] - cnt[child] + cnt.length - cnt[child];
                dfs2(tree, child, cur, cnt, ans);
            }
        }
    }

}

Complexity

  • Time: O(N) - for both dfs
  • Space: O(N)