Sum of Matrix After Queries

Problem

You are given an integer n and a 0-indexed 2D array queries where queries[i] = [typei, indexi, vali].

Initially, there is a 0-indexed n x n matrix filled with 0's. For each query, you must apply one of the following changes:

• if typei == 0, set the values in the row with indexi to vali, overwriting any previous values.
• if typei == 1, set the values in the column with indexi to vali, overwriting any previous values.

Return the sum of integers in the matrix after all queries are applied.

Examples

Example 1

![](https://assets.leetcode.com/uploads/2023/05/11/exm1.png)

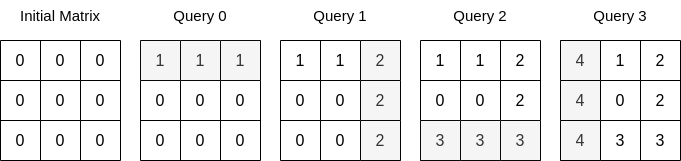
Input: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
Output: 23
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 23. 

Example 2

![](https://assets.leetcode.com/uploads/2023/05/11/exm2.png)

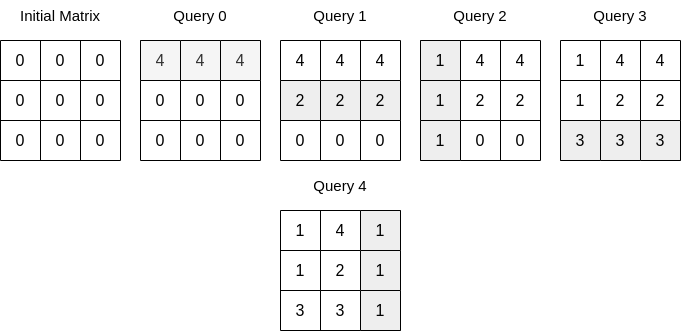
Input: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
Output: 17
Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 17.

Constraints

• 1 <= n <= 10^4
• 1 <= queries.length <= 5 * 10^4
• queries[i].length == 3
• 0 <= typei <= 1
• 0 <= indexi < n
• 0 <= vali <= 10^5

Solution

Approach

Process the queries in reverse. For each row/column, only the last update matters. Track which rows and columns have been set. For each query, if the row/column hasn't been set yet, add its contribution to the answer and mark it as set. Use sets or boolean arrays for efficiency.

---

Code

C++

#include <vector>
#include <unordered_set>
using namespace std;
class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& queries) {
        unordered_set<int> rows, cols;
        long long res = 0;
        for (int i = queries.size()-1; i >= 0; --i) {
            int t = queries[i][0], idx = queries[i][1], val = queries[i][2];
            if (t == 0) {
                if (rows.count(idx)) continue;
                res += 1LL * val * (n - cols.size());
                rows.insert(idx);
            } else {
                if (cols.count(idx)) continue;
                res += 1LL * val * (n - rows.size());
                cols.insert(idx);
            }
        }
        return res;
    }
};

Java

import java.util.*;
class Solution {
    public long matrixSumQueries(int n, int[][] queries) {
        Set<Integer> rows = new HashSet<>(), cols = new HashSet<>();
        long res = 0;
        for (int i = queries.length-1; i >= 0; --i) {
            int t = queries[i][0], idx = queries[i][1], val = queries[i][2];
            if (t == 0) {
                if (rows.contains(idx)) continue;
                res += 1L * val * (n - cols.size());
                rows.add(idx);
            } else {
                if (cols.contains(idx)) continue;
                res += 1L * val * (n - rows.size());
                cols.add(idx);
            }
        }
        return res;
    }
}

Kotlin

class Solution {
    fun matrixSumQueries(n: Int, queries: Array<IntArray>): Long {
        val rows = mutableSetOf<Int>()
        val cols = mutableSetOf<Int>()
        var res = 0L
        for (i in queries.indices.reversed()) {
            val (t, idx, val_) = queries[i]
            if (t == 0) {
                if (rows.contains(idx)) continue
                res += val_ * (n - cols.size)
                rows.add(idx)
            } else {
                if (cols.contains(idx)) continue
                res += val_ * (n - rows.size)
                cols.add(idx)
            }
        }
        return res
    }
}

Python

class Solution:
    def matrixSumQueries(self, n: int, queries: list[list[int]]) -> int:
        rows, cols = set(), set()
        res = 0
        for t, idx, val in reversed(queries):
            if t == 0:
                if idx in rows: continue
                res += val * (n - len(cols))
                rows.add(idx)
            else:
                if idx in cols: continue
                res += val * (n - len(rows))
                cols.add(idx)
        return res

Rust

use std::collections::HashSet;
impl Solution {
    pub fn matrix_sum_queries(n: i32, queries: Vec<Vec<i32>>) -> i64 {
        let mut rows = HashSet::new();
        let mut cols = HashSet::new();
        let mut res = 0i64;
        for q in queries.iter().rev() {
            let t = q[0]; let idx = q[1]; let val = q[2];
            if t == 0 {
                if rows.contains(&idx) { continue; }
                res += val as i64 * (n - cols.len() as i32) as i64;
                rows.insert(idx);
            } else {
                if cols.contains(&idx) { continue; }
                res += val as i64 * (n - rows.len() as i32) as i64;
                cols.insert(idx);
            }
        }
        res
    }
}

TypeScript

function matrixSumQueries(n: number, queries: number[][]): number {
    const rows = new Set<number>(), cols = new Set<number>();
    let res = 0;
    for (let i = queries.length-1; i >= 0; --i) {
        const [t, idx, val] = queries[i];
        if (t === 0) {
            if (rows.has(idx)) continue;
            res += val * (n - cols.size);
            rows.add(idx);
        } else {
            if (cols.has(idx)) continue;
            res += val * (n - rows.size);
            cols.add(idx);
        }
    }
    return res;
}

---

Complexity

• ⏰ Time complexity: O(q) where q is the number of queries
• 🧺 Space complexity: O(n)