Problem

You are given a 0-indexed matrix grid of order n * n. Each cell in this matrix has a value grid[i][j], which is either a positive integer or -1 representing a blocked cell.

You can move from a non-blocked cell to any non-blocked cell that shares an edge.

For any cell (i, j), we represent its remoteness as R[i][j] which is defined as the following:

  • If the cell (i, j) is a non-blocked cell, R[i][j] is the sum of the values grid[x][y] such that there is no path from the non-blocked cell (x, y) to the cell (i, j).
  • For blocked cells, R[i][j] == 0.

Return the sum ofR[i][j]over all cells.

Examples

Example 1:

1
2
3
4
5
6
7

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2800-2899/2852.Sum%20of%20Remoteness%20of%20All%20Cells/images/1-new.png)
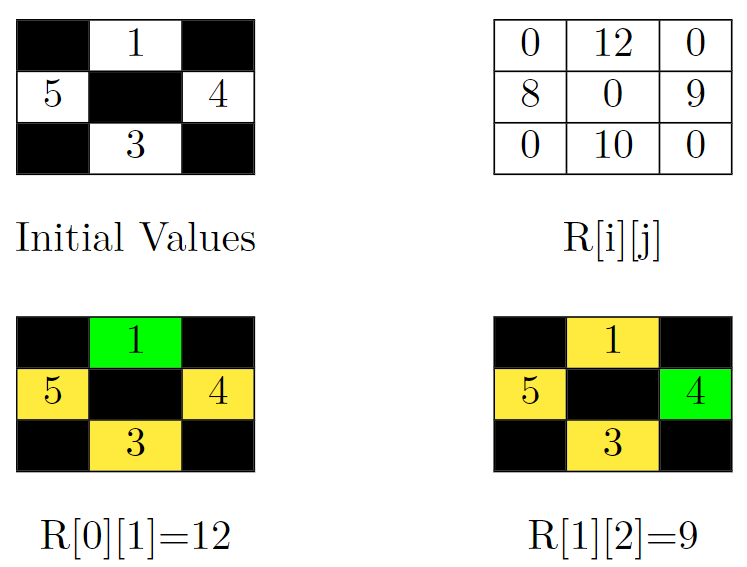
Input: grid = [[-1,1,-1],[5,-1,4],[-1,3,-1]]
Output: 39
Explanation: In the picture above, there are four grids. The top-left grid contains the initial values in the grid. Blocked cells are colored black, and other cells get their values as it is in the input. In the top-right grid, you can see the value of R[i][j] for all cells. So the answer would be the sum of them. That is: 0 + 12 + 0 + 8 + 0 + 9 + 0 + 10 + 0 = 39.
Let's jump on the bottom-left grid in the above picture and calculate R[0][1] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (0, 1). These cells are colored yellow in this grid. So R[0][1] = 5 + 4 + 3 = 12.
Now let's jump on the bottom-right grid in the above picture and calculate R[1][2] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (1, 2). These cells are colored yellow in this grid. So R[1][2] = 1 + 5 + 3 = 9.
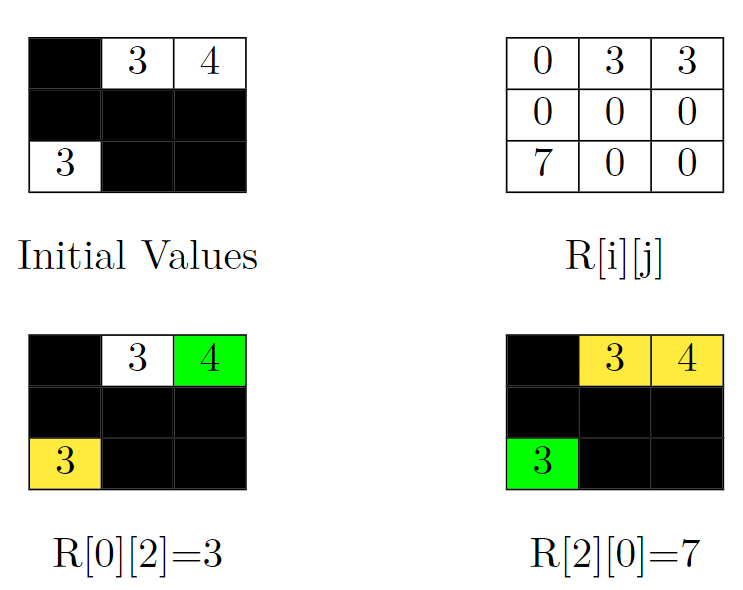
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2800-2899/2852.Sum%20of%20Remoteness%20of%20All%20Cells/images/2.png)

Example 2:

1
2
3
4
5

Input: grid = [[-1,3,4],[-1,-1,-1],[3,-1,-1]]
Output: 13
Explanation: In the picture above, there are four grids. The top-left grid contains the initial values in the grid. Blocked cells are colored black, and other cells get their values as it is in the input. In the top-right grid, you can see the value of R[i][j] for all cells. So the answer would be the sum of them. That is: 3 + 3 + 0 + 0 + 0 + 0 + 7 + 0 + 0 = 13.
Let's jump on the bottom-left grid in the above picture and calculate R[0][2] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (0, 2). This cell is colored yellow in this grid. So R[0][2] = 3.
Now let's jump on the bottom-right grid in the above picture and calculate R[2][0] (the target cell is colored green). We should sum up the value of cells that can't be reached by the cell (2, 0). These cells are colored yellow in this grid. So R[2][0] = 3 + 4 = 7.

Example 3:

1
2
3

Input: grid = [[1]]
Output: 0
Explanation: Since there are no other cells than (0, 0), R[0][0] is equal to 0. So the sum of R[i][j] over all cells would be 0.

Constraints:

  • 1 <= n <= 300
  • 1 <= grid[i][j] <= 10^6 or grid[i][j] == -1

Solution

Approach

First, find all connected components of non-blocked cells using BFS/DFS or union-find, and compute the sum of values in each component. For each non-blocked cell, its remoteness is the sum of all values in other components. For blocked cells, remoteness is 0.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <vector>
#include <queue>
using namespace std;
class Solution {
public:
    int sumRemoteness(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<vector<int>> comp(n, vector<int>(n, -1));
        vector<int> compSum;
        int cid = 0;
        int total = 0;
        vector<pair<int,int>> dirs = {{0,1},{1,0},{0,-1},{-1,0}};
        for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) if (grid[i][j] != -1 && comp[i][j] == -1) {
            int sum = 0;
            queue<pair<int,int>> q;
            q.push({i,j}); comp[i][j] = cid;
            while (!q.empty()) {
                auto [x, y] = q.front(); q.pop();
                sum += grid[x][y];
                for (auto [dx, dy] : dirs) {
                    int nx = x+dx, ny = y+dy;
                    if (nx>=0 && nx<n && ny>=0 && ny<n && grid[nx][ny]!=-1 && comp[nx][ny]==-1) {
                        comp[nx][ny]=cid; q.push({nx,ny});
                    }
                }
            }
            compSum.push_back(sum); total += sum; ++cid;
        }
        int res = 0;
        for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) {
            if (grid[i][j] == -1) continue;
            res += total - compSum[comp[i][j]];
        }
        return res;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import java.util.*;
class Solution {
    public int sumRemoteness(int[][] grid) {
        int n = grid.length;
        int[][] comp = new int[n][n];
        for (int[] row : comp) Arrays.fill(row, -1);
        List<Integer> compSum = new ArrayList<>();
        int cid = 0, total = 0;
        int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
        for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) if (grid[i][j] != -1 && comp[i][j] == -1) {
            int sum = 0;
            Queue<int[]> q = new ArrayDeque<>();
            q.offer(new int[]{i,j}); comp[i][j] = cid;
            while (!q.isEmpty()) {
                int[] cur = q.poll();
                int x = cur[0], y = cur[1];
                sum += grid[x][y];
                for (int[] d : dirs) {
                    int nx = x+d[0], ny = y+d[1];
                    if (nx>=0 && nx<n && ny>=0 && ny<n && grid[nx][ny]!=-1 && comp[nx][ny]==-1) {
                        comp[nx][ny]=cid; q.offer(new int[]{nx,ny});
                    }
                }
            }
            compSum.add(sum); total += sum; ++cid;
        }
        int res = 0;
        for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) {
            if (grid[i][j] == -1) continue;
            res += total - compSum.get(comp[i][j]);
        }
        return res;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import java.util.*
class Solution {
    fun sumRemoteness(grid: Array<IntArray>): Int {
        val n = grid.size
        val comp = Array(n) { IntArray(n) { -1 } }
        val compSum = mutableListOf<Int>()
        var cid = 0
        var total = 0
        val dirs = arrayOf(intArrayOf(0,1), intArrayOf(1,0), intArrayOf(0,-1), intArrayOf(-1,0))
        for (i in 0 until n) for (j in 0 until n) if (grid[i][j] != -1 && comp[i][j] == -1) {
            var sum = 0
            val q: Queue<Pair<Int,Int>> = ArrayDeque()
            q.offer(Pair(i,j)); comp[i][j] = cid
            while (q.isNotEmpty()) {
                val (x, y) = q.poll()
                sum += grid[x][y]
                for (d in dirs) {
                    val nx = x+d[0]; val ny = y+d[1]
                    if (nx in 0 until n && ny in 0 until n && grid[nx][ny]!=-1 && comp[nx][ny]==-1) {
                        comp[nx][ny]=cid; q.offer(Pair(nx,ny))
                    }
                }
            }
            compSum.add(sum); total += sum; ++cid
        }
        var res = 0
        for (i in 0 until n) for (j in 0 until n) {
            if (grid[i][j] == -1) continue
            res += total - compSum[comp[i][j]]
        }
        return res
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

from collections import deque
class Solution:
    def sumRemoteness(self, grid: list[list[int]]) -> int:
        n = len(grid)
        comp = [[-1]*n for _ in range(n)]
        compSum = []
        cid = 0
        total = 0
        dirs = [(0,1),(1,0),(0,-1),(-1,0)]
        for i in range(n):
            for j in range(n):
                if grid[i][j] != -1 and comp[i][j] == -1:
                    q = deque([(i,j)])
                    comp[i][j] = cid
                    s = 0
                    while q:
                        x, y = q.popleft()
                        s += grid[x][y]
                        for dx, dy in dirs:
                            nx, ny = x+dx, y+dy
                            if 0<=nx<n and 0<=ny<n and grid[nx][ny]!=-1 and comp[nx][ny]==-1:
                                comp[nx][ny]=cid; q.append((nx,ny))
                    compSum.append(s); total += s; cid += 1
        res = 0
        for i in range(n):
            for j in range(n):
                if grid[i][j] == -1: continue
                res += total - compSum[comp[i][j]]
        return res
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

use std::collections::VecDeque;
impl Solution {
    pub fn sum_remoteness(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut comp = vec![vec![-1; n]; n];
        let mut comp_sum = vec![];
        let mut cid = 0;
        let mut total = 0;
        let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
        for i in 0..n {
            for j in 0..n {
                if grid[i][j] != -1 && comp[i][j] == -1 {
                    let mut q = VecDeque::new();
                    q.push_back((i,j));
                    comp[i][j] = cid;
                    let mut s = 0;
                    while let Some((x, y)) = q.pop_front() {
                        s += grid[x][y];
                        for (dx, dy) in dirs.iter() {
                            let nx = x as i32 + dx;
                            let ny = y as i32 + dy;
                            if nx>=0 && nx<(n as i32) && ny>=0 && ny<(n as i32) {
                                let nx = nx as usize; let ny = ny as usize;
                                if grid[nx][ny]!=-1 && comp[nx][ny]==-1 {
                                    comp[nx][ny]=cid; q.push_back((nx,ny));
                                }
                            }
                        }
                    }
                    comp_sum.push(s); total += s; cid += 1;
                }
            }
        }
        let mut res = 0;
        for i in 0..n {
            for j in 0..n {
                if grid[i][j] == -1 { continue; }
                res += total - comp_sum[comp[i][j] as usize];
            }
        }
        res
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

function sumRemoteness(grid: number[][]): number {
    const n = grid.length;
    const comp: number[][] = Array.from({length: n}, () => Array(n).fill(-1));
    const compSum: number[] = [];
    let cid = 0, total = 0;
    const dirs = [[0,1],[1,0],[0,-1],[-1,0]];
    for (let i = 0; i < n; ++i) for (let j = 0; j < n; ++j) if (grid[i][j] !== -1 && comp[i][j] === -1) {
        let sum = 0;
        const q: [number, number][] = [[i,j]]; comp[i][j] = cid;
        while (q.length) {
            const [x, y] = q.shift()!;
            sum += grid[x][y];
            for (const [dx, dy] of dirs) {
                const nx = x+dx, ny = y+dy;
                if (nx>=0 && nx<n && ny>=0 && ny<n && grid[nx][ny]!==-1 && comp[nx][ny]===-1) {
                    comp[nx][ny]=cid; q.push([nx,ny]);
                }
            }
        }
        compSum.push(sum); total += sum; ++cid;
    }
    let res = 0;
    for (let i = 0; i < n; ++i) for (let j = 0; j < n; ++j) {
        if (grid[i][j] === -1) continue;
        res += total - compSum[comp[i][j]];
    }
    return res;
}

Complexity

  • ⏰ Time complexity: O(n^2)
  • 🧺 Space complexity: O(n^2)