Tiling a Rectangle with the Fewest Squares
HardUpdated: Aug 2, 2025
Practice on:
Problem
Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.
Examples
Example 1
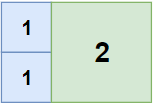
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)
Example 2
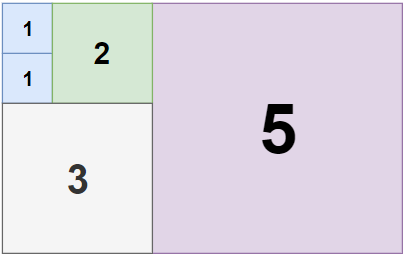
Input: n = 5, m = 8
Output: 5
Example 3
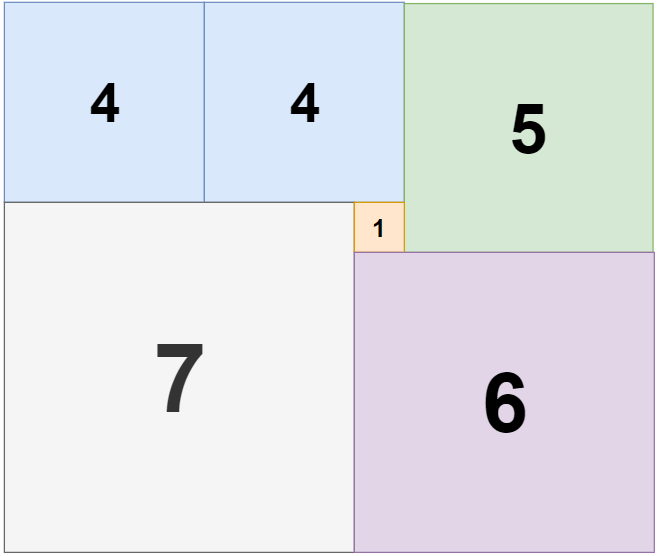
Input: n = 11, m = 13
Output: 6
Constraints
1 <= n, m <= 13
Solution
Method 1 – Backtracking with Pruning
Intuition
Try to fill the rectangle greedily with the largest possible square at each step, backtracking and pruning when the current path cannot improve the best answer found so far.
Approach
Use DFS/backtracking. At each step, find the first empty cell, try all possible square sizes, fill, recurse, and backtrack. Prune if the current count exceeds the best found.
Code
C++
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int res = INT_MAX;
int tilingRectangle(int n, int m) {
vector<vector<int>> rect(n, vector<int>(m));
dfs(rect, 0);
return res;
}
void dfs(vector<vector<int>>& rect, int cnt) {
int n = rect.size(), m = rect[0].size();
if (cnt >= res) return;
int x = -1, y = -1;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (rect[i][j] == 0) {
x = i; y = j;
goto found;
}
}
}
res = min(res, cnt);
return;
found:
int maxLen = min(n - x, m - y);
for (int k = maxLen; k >= 1; --k) {
bool canFill = true;
for (int i = 0; i < k && canFill; ++i)
for (int j = 0; j < k && canFill; ++j)
if (rect[x + i][y + j]) canFill = false;
if (!canFill) continue;
for (int i = 0; i < k; ++i)
for (int j = 0; j < k; ++j)
rect[x + i][y + j] = 1;
dfs(rect, cnt + 1);
for (int i = 0; i < k; ++i)
for (int j = 0; j < k; ++j)
rect[x + i][y + j] = 0;
}
}
};
Java
import java.util.*;
public class Solution {
private int res = Integer.MAX_VALUE;
public int tilingRectangle(int n, int m) {
int[][] rect = new int[n][m];
dfs(rect, 0);
return res;
}
private void dfs(int[][] rect, int cnt) {
int n = rect.length, m = rect[0].length;
if (cnt >= res) return;
int x = -1, y = -1;
outer:
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (rect[i][j] == 0) {
x = i; y = j;
break outer;
}
}
}
if (x == -1) {
res = Math.min(res, cnt);
return;
}
int maxLen = Math.min(n - x, m - y);
for (int k = maxLen; k >= 1; --k) {
boolean canFill = true;
for (int i = 0; i < k && canFill; ++i)
for (int j = 0; j < k && canFill; ++j)
if (rect[x + i][y + j] != 0) canFill = false;
if (!canFill) continue;
for (int i = 0; i < k; ++i)
for (int j = 0; j < k; ++j)
rect[x + i][y + j] = 1;
dfs(rect, cnt + 1);
for (int i = 0; i < k; ++i)
for (int j = 0; j < k; ++j)
rect[x + i][y + j] = 0;
}
}
}
Python
class Solution:
def tilingRectangle(self, n: int, m: int) -> int:
self.res = n * m
rect = [[0] * m for _ in range(n)]
def dfs(cnt):
if cnt >= self.res:
return
for i in range(n):
for j in range(m):
if rect[i][j] == 0:
x, y = i, j
break
else:
continue
break
else:
self.res = min(self.res, cnt)
return
max_len = min(n - x, m - y)
for k in range(max_len, 0, -1):
can_fill = True
for dx in range(k):
for dy in range(k):
if rect[x + dx][y + dy]:
can_fill = False
break
if not can_fill:
break
if not can_fill:
continue
for dx in range(k):
for dy in range(k):
rect[x + dx][y + dy] = 1
dfs(cnt + 1)
for dx in range(k):
for dy in range(k):
rect[x + dx][y + dy] = 0
dfs(0)
return self.res
Rust
impl Solution {
pub fn tiling_rectangle(n: i32, m: i32) -> i32 {
fn dfs(rect: &mut Vec<Vec<i32>>, cnt: i32, res: &mut i32) {
let n = rect.len();
let m = rect[0].len();
if cnt >= *res { return; }
let mut x = None;
let mut y = None;
'outer: for i in 0..n {
for j in 0..m {
if rect[i][j] == 0 {
x = Some(i); y = Some(j);
break 'outer;
}
}
}
if x.is_none() {
*res = cnt.min(*res);
return;
}
let x = x.unwrap();
let y = y.unwrap();
let max_len = n.min(m).min(n - x).min(m - y);
for k in (1..=max_len).rev() {
let mut can_fill = true;
'check: for dx in 0..k {
for dy in 0..k {
if rect[x + dx][y + dy] != 0 {
can_fill = false;
break 'check;
}
}
}
if !can_fill { continue; }
for dx in 0..k {
for dy in 0..k {
rect[x + dx][y + dy] = 1;
}
}
dfs(rect, cnt + 1, res);
for dx in 0..k {
for dy in 0..k {
rect[x + dx][y + dy] = 0;
}
}
}
}
let n = n as usize;
let m = m as usize;
let mut rect = vec![vec![0; m]; n];
let mut res = (n * m) as i32;
dfs(&mut rect, 0, &mut res);
res
}
}
TypeScript
function tilingRectangle(n: number, m: number): number {
let res = n * m;
const rect = Array.from({ length: n }, () => Array(m).fill(0));
function dfs(cnt: number) {
if (cnt >= res) return;
let x = -1, y = -1;
outer: for (let i = 0; i < n; ++i) {
for (let j = 0; j < m; ++j) {
if (rect[i][j] === 0) {
x = i; y = j;
break outer;
}
}
}
if (x === -1) {
res = Math.min(res, cnt);
return;
}
let maxLen = Math.min(n - x, m - y);
for (let k = maxLen; k >= 1; --k) {
let canFill = true;
for (let dx = 0; dx < k && canFill; ++dx) {
for (let dy = 0; dy < k && canFill; ++dy) {
if (rect[x + dx][y + dy]) canFill = false;
}
}
if (!canFill) continue;
for (let dx = 0; dx < k; ++dx)
for (let dy = 0; dy < k; ++dy)
rect[x + dx][y + dy] = 1;
dfs(cnt + 1);
for (let dx = 0; dx < k; ++dx)
for (let dy = 0; dy < k; ++dy)
rect[x + dx][y + dy] = 0;
}
}
dfs(0);
return res;
}
Complexity
- ⏰ Time complexity:
O((nm)!)(worst case, but pruned heavily) - 🧺 Space complexity:
O(nm)