problemhardalgorithmsleetcode-3241leetcode 3241leetcode3241

Time Taken to Mark All Nodes

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree.

Initially, all nodes are unmarked. For each node i:

  • If i is odd, the node will get marked at time x if there is at least one node adjacent to it which was marked at time x - 1.
  • If i is even, the node will get marked at time x if there is at least one node adjacent to it which was marked at time x - 2.

Return an array times where times[i] is the time when all nodes get marked in the tree, if you mark node i at time t = 0.

Note that the answer for each times[i] is independent , i.e. when you mark node i all other nodes are unmarked.

Examples

Example 1


Input: edges = [[0,1],[0,2]]

Output: [2,4,3]

Explanation:

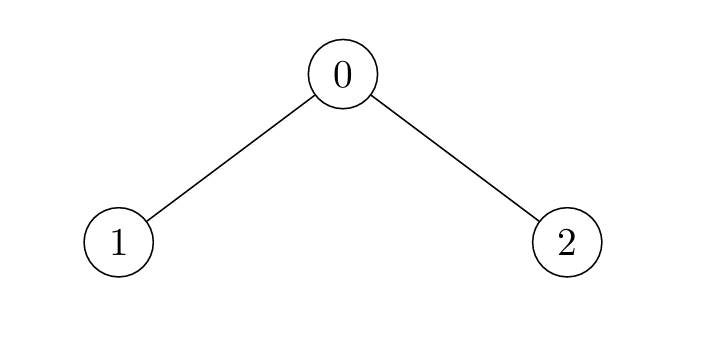
![](https://assets.leetcode.com/uploads/2024/06/01/screenshot-2024-06-02-122236.png)

  * For `i = 0`: 
  * Node 1 is marked at `t = 1`, and Node 2 at `t = 2`.
  * For `i = 1`: 
  * Node 0 is marked at `t = 2`, and Node 2 at `t = 4`.
  * For `i = 2`: 
  * Node 0 is marked at `t = 2`, and Node 1 at `t = 3`.

Example 2


Input: edges = [[0,1]]

Output: [1,2]

Explanation:

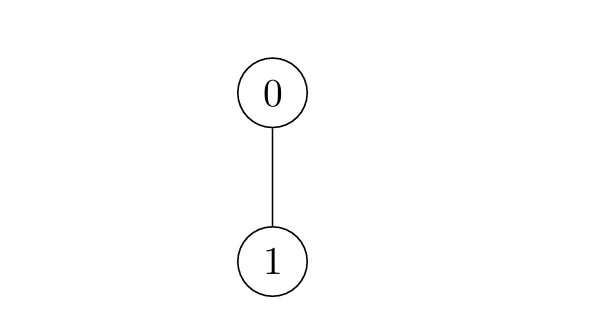
![](https://assets.leetcode.com/uploads/2024/06/01/screenshot-2024-06-02-122249.png)

  * For `i = 0`: 
  * Node 1 is marked at `t = 1`.
  * For `i = 1`: 
  * Node 0 is marked at `t = 2`.

Example 3


Input: edges = [[2,4],[0,1],[2,3],[0,2]]

Output: [4,6,3,5,5]

Explanation:

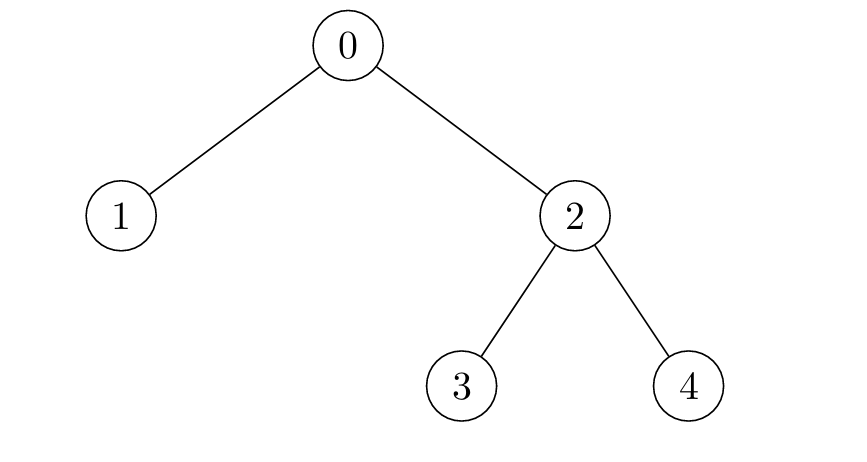
![](https://assets.leetcode.com/uploads/2024/06/03/screenshot-2024-06-03-210550.png)

Constraints

  • 2 <= n <= 10^5
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • The input is generated such that edges represents a valid tree.

Solution

Method 1 – BFS with Parity-Dependent Propagation

Intuition

For each node as the root, perform BFS, propagating marks according to the node's parity. Use a queue and track the earliest time each node can be marked.

Approach

For each node, run BFS. If the current node is odd, neighbors are marked at t+1; if even, at t+2. Track the maximum time for each run.

Code

Python
from collections import deque, defaultdict
from typing import List
class Solution:
    def minimumTimeToMarkAllNodes(self, n: int, edges: List[List[int]]) -> List[int]:
        g = [[] for _ in range(n)]
        for u, v in edges:
            g[u].append(v)
            g[v].append(u)
        res = [0] * n
        for start in range(n):
            time = [float('inf')] * n
            time[start] = 0
            q = deque([start])
            while q:
                u = q.popleft()
                for v in g[u]:
                    d = 1 if u % 2 else 2
                    if time[v] > time[u] + d:
                        time[v] = time[u] + d
                        q.append(v)
            res[start] = max(time)
        return res
Java
import java.util.*;
class Solution {
    public int[] minimumTimeToMarkAllNodes(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        int[] res = new int[n];
        for (int start = 0; start < n; ++start) {
            int[] time = new int[n];
            Arrays.fill(time, Integer.MAX_VALUE);
            time[start] = 0;
            Queue<Integer> q = new ArrayDeque<>();
            q.offer(start);
            while (!q.isEmpty()) {
                int u = q.poll();
                for (int v : g[u]) {
                    int d = (u % 2 == 0) ? 2 : 1;
                    if (time[v] > time[u] + d) {
                        time[v] = time[u] + d;
                        q.offer(v);
                    }
                }
            }
            int mx = 0;
            for (int t : time) mx = Math.max(mx, t);
            res[start] = mx;
        }
        return res;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2)
  • 🧺 Space complexity: O(n^2)

Comments