Time to Cross a Bridge
Problem
There are k workers who want to move n boxes from the right (old) warehouse to the left (new) warehouse. You are given the two integers n and
k, and a 2D integer array time of size k x 4 where time[i] = [righti, picki, lefti, puti].
The warehouses are separated by a river and connected by a bridge. Initially, all k workers are waiting on the left side of the bridge. To move the boxes, the ith worker can do the following:
- Cross the bridge to the right side in
rightiminutes. - Pick a box from the right warehouse in
pickiminutes. - Cross the bridge to the left side in
leftiminutes. - Put the box into the left warehouse in
putiminutes.
The ith worker is less efficient than the jth worker if either condition is met:
lefti + righti > leftj + rightjlefti + righti == leftj + rightjandi > j
The following rules regulate the movement of the workers through the bridge:
- Only one worker can use the bridge at a time.
- When the bridge is unused prioritize the least efficient worker (who have picked up the box) on the right side to cross. If not, prioritize the least efficient worker on the left side to cross.
- If enough workers have already been dispatched from the left side to pick up all the remaining boxes, no more workers will be sent from the left side.
Return the elapsed minutes at which the last box reaches the left side of the bridge.
Examples
Example 1
Input: n = 1, k = 3, time = [[1,1,2,1],[1,1,3,1],[1,1,4,1]]
Output: 6
Explanation:
From 0 to 1 minutes: worker 2 crosses the bridge to the right.
From 1 to 2 minutes: worker 2 picks up a box from the right warehouse.
From 2 to 6 minutes: worker 2 crosses the bridge to the left.
From 6 to 7 minutes: worker 2 puts a box at the left warehouse.
The whole process ends after 7 minutes. We return 6 because the problem asks for the instance of time at which the last worker reaches the left side of the bridge.
Example 2
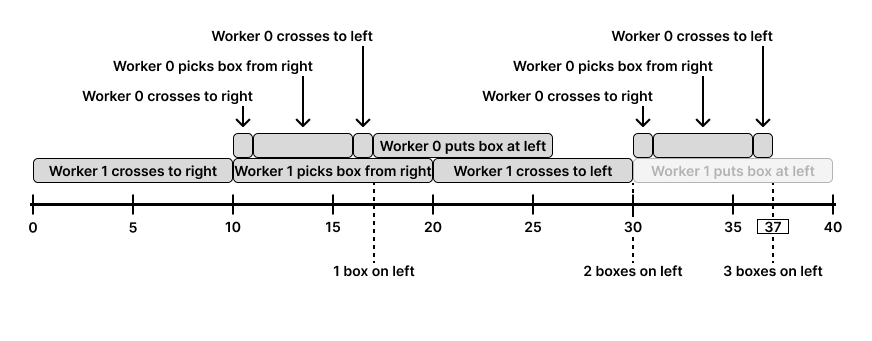
Input: n = 3, k = 2, time = [[1,5,1,8],[10,10,10,10]]
Output: 37
Explanation:
The last box reaches the left side at 37 seconds. Notice, how we **do not**
put the last boxes down, as that would take more time, and they are already on
the left with the workers.
Constraints
1 <= n, k <= 10^4time.length == ktime[i].length == 41 <= lefti, picki, righti, puti <= 1000
Solution
Method 1 – Simulation with Priority Queues
Intuition
Simulate the process using priority queues to manage the workers on both sides, always picking the least efficient worker as required.
Approach
Use heaps to track available workers on each side, and simulate the process step by step, always prioritizing the least efficient worker as per the rules.
Code
Python
import heapq
from typing import List
class Solution:
def findCrossingTime(self, n: int, k: int, time: List[List[int]]) -> int:
left = [(-(time[i][0] + time[i][2]), -i, i, 0) for i in range(k)] # (efficiency, -index, worker, available_time)
heapq.heapify(left)
right = [] # (efficiency, -index, worker, available_time)
wait_left, wait_right = [], [] # (available_time, efficiency, -index, worker)
cur_time = 0
boxes = n
while boxes > 0 or right or wait_right:
# Move workers from wait queues to ready queues if available
while wait_left and wait_left[0][0] <= cur_time:
_, eff, idx, w = heapq.heappop(wait_left)
heapq.heappush(left, (eff, idx, w, cur_time))
while wait_right and wait_right[0][0] <= cur_time:
_, eff, idx, w = heapq.heappop(wait_right)
heapq.heappush(right, (eff, idx, w, cur_time))
# If right side has workers, they cross first
if right:
eff, idx, w, _ = heapq.heappop(right)
cur_time += time[w][2]
heapq.heappush(wait_left, (cur_time + time[w][3], eff, idx, w))
elif boxes > 0 and left:
eff, idx, w, _ = heapq.heappop(left)
cur_time += time[w][0]
heapq.heappush(wait_right, (cur_time + time[w][1], eff, idx, w))
boxes -= 1
else:
# Advance time to next available worker
next_times = []
if wait_left: next_times.append(wait_left[0][0])
if wait_right: next_times.append(wait_right[0][0])
if next_times:
cur_time = max(cur_time, min(next_times))
return cur_time
Java
import java.util.*;
class Solution {
public int findCrossingTime(int n, int k, int[][] time) {
PriorityQueue<int[]> left = new PriorityQueue<>((a, b) -> a[0] != b[0] ? b[0] - a[0] : b[1] - a[1]);
PriorityQueue<int[]> right = new PriorityQueue<>((a, b) -> a[0] != b[0] ? b[0] - a[0] : b[1] - a[1]);
PriorityQueue<int[]> waitLeft = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
PriorityQueue<int[]> waitRight = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
for (int i = 0; i < k; ++i) left.offer(new int[]{time[i][0] + time[i][2], i, i, 0});
int curTime = 0, boxes = n;
while (boxes > 0 || !right.isEmpty() || !waitRight.isEmpty()) {
while (!waitLeft.isEmpty() && waitLeft.peek()[0] <= curTime) {
int[] arr = waitLeft.poll();
left.offer(new int[]{arr[1], arr[2], arr[3], curTime});
}
while (!waitRight.isEmpty() && waitRight.peek()[0] <= curTime) {
int[] arr = waitRight.poll();
right.offer(new int[]{arr[1], arr[2], arr[3], curTime});
}
if (!right.isEmpty()) {
int[] arr = right.poll();
curTime += time[arr[2]][2];
waitLeft.offer(new int[]{curTime + time[arr[2]][3], arr[0], arr[1], arr[2]});
} else if (boxes > 0 && !left.isEmpty()) {
int[] arr = left.poll();
curTime += time[arr[2]][0];
waitRight.offer(new int[]{curTime + time[arr[2]][1], arr[0], arr[1], arr[2]});
boxes--;
} else {
int next = Integer.MAX_VALUE;
if (!waitLeft.isEmpty()) next = Math.min(next, waitLeft.peek()[0]);
if (!waitRight.isEmpty()) next = Math.min(next, waitRight.peek()[0]);
if (next != Integer.MAX_VALUE) curTime = Math.max(curTime, next);
}
}
return curTime;
}
}
Complexity
- ⏰ Time complexity:
O((n+k) log k) - 🧺 Space complexity:
O(k)