Transpose of a Matrix
Problem
Given a 2D integer array matrix, return the transpose of matrix.
The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
Examples
Example 1:
Input:
matrix =[[1,2,3],[4,5,6],[7,8,9]]
Output:
[[1,4,7],[2,5,8],[3,6,9]]
Example 2:
Input:
matrix =[[1,2,3],[4,5,6]]
Output:
[[1,4],[2,5],[3,6]]
Follow up
Can we do it in-place?
How the transpose works
The transpose of a matrix is found by flipping the matrix over its diagonal, i.e. by exchanging the rows and columns.
Lets look at some example:
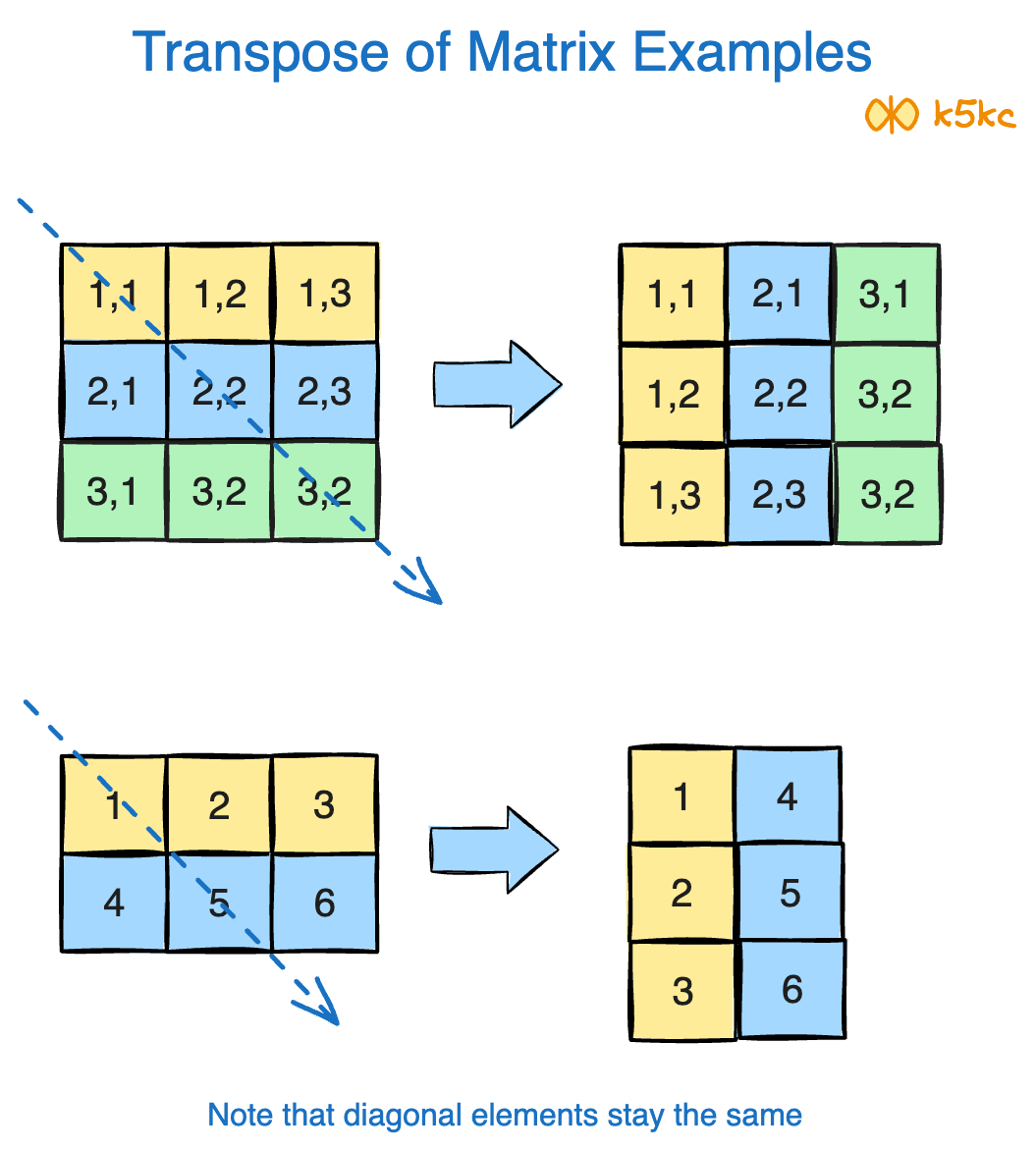
More examples:
Solution
Method 1 - Using Aux Array
Step 1 : Create an auxiliary dummy matrix which stores the transpose of the matrix.
Step 2 : For a row in the first matrix, make it as first column in new constructed matrix.
Step 3 : move to next row and do it for all the rows.
B[i][j] = A[j][i] , B is Transpose of A
Step 4 : After completing all the rows, print the new matrix, it is Transpose of the given matrix.
Code
Java
public int[][] transpose(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int[][] T = new int[n][m];
for (int i = 0; i<m; i++) {
for (int j = 0; j<n; j++) {
T[j][i] = matrix[i][j];
}
}
return T;
}
Method 2 - Doing it in Place
In java, when a matrix is created, its size is fixed.
But if it is square matrix, in-place works.
To swap upper half of the main diagonal of matrix with the lower half. We have to traverse only in upper half.
More precisely, if a cell present at (i, j) in upper half of the main diagonal then we can get its corresponding lower half cell at (j, i).
So our main focus should be traversing to upper half of the main diagonal.
While traversing upper half : swap(matrix[i][j], matrix[j][i])
Code
Java
public int[][] transposeSquare(int[][] matrix) {
for(int i = 0; i < matrix.length; i += 1) {
for(int j = i + 1; j < matrix[0].length; j += 1) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
return matrix;
}
Clubbing Method 1 and Method 2:
public int[][] transpose(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
if (m == n) {
return transposeSquare(matrix);
}
int[][] T = new int[n][m];
for (int i = 0; i<m; i++) {
for (int j = 0; j<n; j++) {
T[j][i] = matrix[i][j];
}
}
return T;
}