Trapping Rain Water 2

Problem

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

Examples

Example 1:

1
2
3
4
5
6
7


Input:
heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output:
 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

1
2
3
4


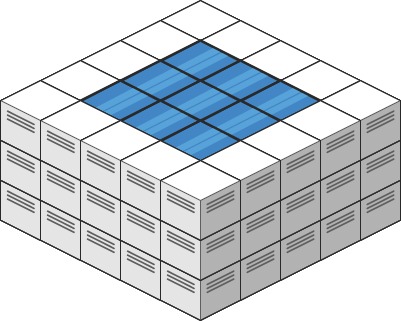
Input:
heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output:
 10

Constraints:

m == heightMap.length
n == heightMap[i].length
1 <= m, n <= 200
0 <= heightMap[i][j] <= 2 * 10^4

Solution

Method 1 – Priority Queue (Min-Heap) + BFS

Intuition

The key idea is to treat the 2D elevation map like a container with boundaries. Water can only be trapped if it is surrounded by higher boundaries. By always processing the lowest boundary first (using a min-heap), we ensure that we never overestimate the water level at any cell. As we expand inward from the boundary, we update the water level based on the minimum height of the surrounding walls, similar to how water would naturally fill up the lowest spots first.

Approach

Initialization:
- If the matrix is empty or too small, return 0.
- Mark all boundary cells as visited and add them to a min-heap (priority queue) with their heights.
Processing:
- While the heap is not empty:
  - Pop the cell with the lowest height.
  - For each of its four neighbors (up, down, left, right):
    - If the neighbor is within bounds and not visited:
      - Mark it as visited.
      - If the neighbor’s height is lower than the current cell’s height, water can be trapped. Add the difference to the answer.
      - Push the neighbor into the heap with the maximum of its own height and the current cell’s height (to maintain the correct boundary for future cells).
Edge Cases:
- Handle empty or single-row/column matrices.
- Ensure all boundary cells are processed first to prevent water from leaking out.
Return:
- The total trapped water after processing all cells.

Code

1
2

##### C++

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45


class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        if(heightMap.empty() || heightMap[0].empty()) return 0;
        
        int m = heightMap.size();
        int n = heightMap[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        auto comp = [](const vector<int>& a, const vector<int>& b) {
            return a[2] > b[2];
        };
        priority_queue<vector<int>, vector<vector<int>>, decltype(comp)> pq(comp);
        
        for(int i = 0; i < m; ++i) {
            pq.push({i, 0, heightMap[i][0]});
            pq.push({i, n - 1, heightMap[i][n - 1]});
            visited[i][0] = visited[i][n - 1] = true;
        }
        
        for(int j = 0; j < n; ++j) {
            pq.push({0, j, heightMap[0][j]});
            pq.push({m - 1, j, heightMap[m - 1][j]});
            visited[0][j] = visited[m - 1][j] = true;
        }
        
        int ans = 0;
        vector<int> dirs = {-1, 0, 1, 0, -1};
        
        while(!pq.empty()) {
            auto cell = pq.top();
            pq.pop();
            for(int k = 0; k < 4; ++k) {
                int x = cell[0] + dirs[k];
                int y = cell[1] + dirs[k + 1];
                if(x >= 0 && x < m && y >= 0 && y < n && !visited[x][y]) {
                    visited[x][y] = true;
                    ans += max(0, cell[2] - heightMap[x][y]);
                    pq.push({x, y, max(cell[2], heightMap[x][y])});
                }
            }
        }
        
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73


type Cell struct {
    x, y, h int
}

type MinHeap []Cell

func (h MinHeap) Len() int           { return len(h) }
func (h MinHeap) Less(i, j int) bool { return h[i].h < h[j].h }
func (h MinHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
func (h *MinHeap) Push(x interface{}) {
    *h = append(*h, x.(Cell))
}
func (h *MinHeap) Pop() interface{} {
    old := *h
    n := len(old)
    x := old[n-1]
    *h = old[0 : n-1]
    return x
}

func trapRainWater(heightMap [][]int) int {
    if len(heightMap) == 0 || len(heightMap[0]) == 0 {
        return 0
    }

    m, n := len(heightMap), len(heightMap[0])
    visited := make([][]bool, m)
    for i := 0; i < m; i++ {
        visited[i] = make([]bool, n)
    }

    h := &MinHeap{}
    heap.Init(h)
    for i := 0; i < m; i++ {
        heap.Push(h, Cell{i, 0, heightMap[i][0]})
        heap.Push(h, Cell{i, n - 1, heightMap[i][n - 1]})
        visited[i][0] = true
        visited[i][n-1] = true
    }

    for j := 0; j < n; j++ {
        heap.Push(h, Cell{0, j, heightMap[0][j]})
        heap.Push(h, Cell{m - 1, j, heightMap[m-1][j]})
        visited[0][j] = true
        visited[m-1][j] = true
    }

    ans := 0
    dirs := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}

    for h.Len() > 0 {
        cell := heap.Pop(h).(Cell)
        for _, d := range dirs {
            x, y := cell.x+d[0], cell.y+d[1]
            if x >= 0 && x < m && y >= 0 && y < n && !visited[x][y] {
                visited[x][y] = true
                if cell.h > heightMap[x][y] {
                    ans += cell.h - heightMap[x][y]
                }
                heap.Push(h, Cell{x, y, max(cell.h, heightMap[x][y])})
            }
        }
    }

    return ans
}
 
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


class Solution {
    public int trapRainWater(int[][] heightMap) {
        int m = heightMap.length, n = heightMap[0].length;
        boolean[][] visited = new boolean[m][n];
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> Integer.compare(a[2], b[2]));
        
        for (int i = 0; i < m; i++) {
            visited[i][0] = true;
            visited[i][n - 1] = true;
            pq.offer(new int[]{i, 0, heightMap[i][0]});
            pq.offer(new int[]{i, n - 1, heightMap[i][n - 1]});
        }
        
        for (int j = 0; j < n; j++) {
            visited[0][j] = true;
            visited[m - 1][j] = true;
            pq.offer(new int[]{0, j, heightMap[0][j]});
            pq.offer(new int[]{m - 1, j, heightMap[m - 1][j]});
        }

        int[] dirs = {-1, 0, 1, 0, -1};
        int ans = 0;

        while (!pq.isEmpty()) {
            int[] cell = pq.poll();
            for (int k = 0; k < 4; k++) {
                int x = cell[0] + dirs[k];
                int y = cell[1] + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && !visited[x][y]) {
                    visited[x][y] = true;
                    ans += Math.max(0, cell[2] - heightMap[x][y]);
                    pq.offer(new int[]{x, y, Math.max(cell[2], heightMap[x][y])});
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


 class Solution:
     def trapRainWater(self, heightMap: List[List[int]]) -> int:
         if not heightMap or not heightMap[0]:
             return 0
         
         m, n = len(heightMap), len(heightMap[0])
         visited = [[False] * n for _ in range(m)]
         pq = []
         
         for i in range(m):
             visited[i][0] = visited[i][n - 1] = True
             heappush(pq, (heightMap[i][0], i, 0))
             heappush(pq, (heightMap[i][n - 1], i, n - 1))
         
         for j in range(n):
             visited[0][j] = visited[m - 1][j] = True
             heappush(pq, (heightMap[0][j], 0, j))
             heappush(pq, (heightMap[m - 1][j], m - 1, j))
         
         ans = 0
         dirs = [(-1, 0), (1, 0), (0, -1), (0, 1)]
         
         while pq:
             h, x, y = heappop(pq)
             for dx, dy in dirs:
                 nx, ny = x + dx, y + dy
                 if 0 <= nx < m and 0 <= ny < n and not visited[nx][ny]:
                     visited[nx][ny] = True
                     ans += max(0, h - heightMap[nx][ny])
                     heappush(pq, (max(h, heightMap[nx][ny]), nx, ny))
         
         return ans

Complexity

Time: O(m × n × log(mn)), where m and n are the matrix dimensions. Each cell is pushed and popped from the heap once, and heap operations take log(mn) time.
Space: O(m × n) for the visited matrix and the heap.

Problem#

Examples#

Solution#

Method 1 – Priority Queue (Min-Heap) + BFS#

Intuition#

Approach#

Code#

Complexity#