Tree Diameter

Problem

The diameter of a tree is the number of edges in the longest path in that tree.

There is an undirected tree of n nodes labeled from 0 to n - 1. You are given a 2D array edges where edges.length == n - 1 and edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the tree.

Return thediameter of the tree.

Examples

Example 1:

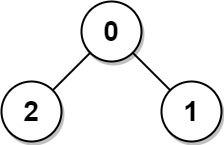
Input: edges = [[0,1],[0,2]]
Output: 2
Explanation: The longest path of the tree is the path 1 - 0 - 2.

Example 2:

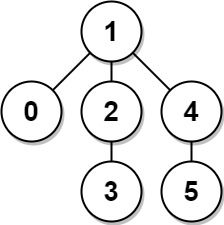
Input: edges = [[0,1],[1,2],[2,3],[1,4],[4,5]]
Output: 4
Explanation: The longest path of the tree is the path 3 - 2 - 1 - 4 - 5.

Constraints:

• n == edges.length + 1
• 1 <= n <= 10^4
• 0 <= ai, bi < n
• ai != bi

Solution

Method 1 – Double DFS/BFS

Intuition

The diameter of a tree can be found by:

1. Pick any node and perform DFS/BFS to find the farthest node A.
2. From A, perform DFS/BFS again to find the farthest node B. The distance between A and B is the diameter.

Approach

We build the adjacency list for the tree, then use DFS (or BFS) twice as described above. This works because the longest path in a tree always lies between two leaf nodes.

Code

C++

#include <vector>
#include <queue>
using namespace std;

class Solution {
public:
    int treeDiameter(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        auto bfs = [&](int start) {
            vector<int> dist(n, -1);
            queue<int> q;
            q.push(start);
            dist[start] = 0;
            int far = start;
            while (!q.empty()) {
                int u = q.front(); q.pop();
                for (int v : g[u]) {
                    if (dist[v] == -1) {
                        dist[v] = dist[u] + 1;
                        q.push(v);
                        if (dist[v] > dist[far]) far = v;
                    }
                }
            }
            return make_pair(far, dist[far]);
        };
        int u = bfs(0).first;
        return bfs(u).second;
    }
};

Java

import java.util.*;
class Solution {
    public int treeDiameter(int[][] edges) {
        int n = edges.length + 1;
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        int[] res = bfs(g, 0);
        res = bfs(g, res[0]);
        return res[1];
    }
    private int[] bfs(List<List<Integer>> g, int start) {
        int n = g.size();
        int[] dist = new int[n];
        Arrays.fill(dist, -1);
        Queue<Integer> q = new LinkedList<>();
        q.offer(start);
        dist[start] = 0;
        int far = start;
        while (!q.isEmpty()) {
            int u = q.poll();
            for (int v : g.get(u)) {
                if (dist[v] == -1) {
                    dist[v] = dist[u] + 1;
                    q.offer(v);
                    if (dist[v] > dist[far]) far = v;
                }
            }
        }
        return new int[]{far, dist[far]};
    }
}

Python

from collections import deque, defaultdict
class Solution:
    def treeDiameter(self, edges):
        n = len(edges) + 1
        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        def bfs(start):
            dist = [-1] * n
            q = deque([start])
            dist[start] = 0
            far = start
            while q:
                u = q.popleft()
                for v in g[u]:
                    if dist[v] == -1:
                        dist[v] = dist[u] + 1
                        q.append(v)
                        if dist[v] > dist[far]:
                            far = v
            return far, dist[far]
        u, _ = bfs(0)
        _, d = bfs(u)
        return d

Rust

use std::collections::VecDeque;
impl Solution {
    pub fn tree_diameter(edges: Vec<Vec<i32>>) -> i32 {
        let n = edges.len() + 1;
        let mut g = vec![vec![]; n];
        for e in edges.iter() {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        fn bfs(g: &Vec<Vec<usize>>, start: usize) -> (usize, i32) {
            let n = g.len();
            let mut dist = vec![-1; n];
            let mut q = VecDeque::new();
            q.push_back(start);
            dist[start] = 0;
            let mut far = start;
            while let Some(u) = q.pop_front() {
                for &v in &g[u] {
                    if dist[v] == -1 {
                        dist[v] = dist[u] + 1;
                        q.push_back(v);
                        if dist[v] > dist[far] {
                            far = v;
                        }
                    }
                }
            }
            (far, dist[far])
        }
        let u = bfs(&g, 0).0;
        bfs(&g, u).1
    }
}

TypeScript

function treeDiameter(edges: number[][]): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({length: n}, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    function bfs(start: number): [number, number] {
        const dist = Array(n).fill(-1);
        const q: number[] = [start];
        dist[start] = 0;
        let far = start;
        while (q.length) {
            const u = q.shift()!;
            for (const v of g[u]) {
                if (dist[v] === -1) {
                    dist[v] = dist[u] + 1;
                    q.push(v);
                    if (dist[v] > dist[far]) far = v;
                }
            }
        }
        return [far, dist[far]];
    }
    const [u] = bfs(0);
    const [, d] = bfs(u);
    return d;
}

Complexity

• ⏰ Time complexity: O(n)
• 🧺 Space complexity: O(n)