problemmediumalgorithmsleetcode-1214leetcode 1214leetcode1214

Two Sum BSTs

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given the roots of two binary search trees, root1 and root2, return true if and only if there is a node in the first tree and a node in the second tree whose values sum up to a given integer target.

Examples

Example 1:

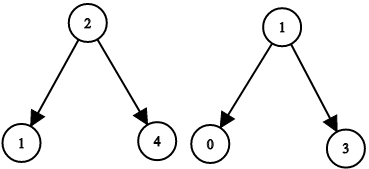
Input: root1 = [2,1,4], root2 = [1,0,3], target = 5
Output: true
Explanation: 2 and 3 sum up to 5.

Example 2:

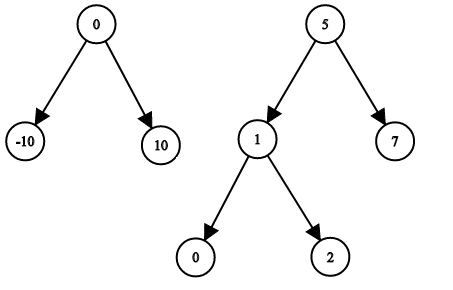
Input: root1 = [0,-10,10], root2 = [5,1,7,0,2], target = 18
Output: false

Constraints:

  • The number of nodes in each tree is in the range [1, 5000].
  • -10^9 <= Node.val, target <= 10^9

Solution

Method 1 – Hash Set or Inorder Traversal

Intuition

Store all values from one tree in a set, then for each node in the other tree, check if target - node.val exists in the set.

Approach

  1. Traverse root1 and store all values in a set.
  2. Traverse root2 and for each node, check if target - node.val is in the set.
  3. Return true if found, else false.

Code

Java
import java.util.*;
class Solution {
    public boolean twoSumBSTs(TreeNode root1, TreeNode root2, int target) {
        Set<Integer> set = new HashSet<>();
        fill(root1, set);
        return find(root2, set, target);
    }
    void fill(TreeNode node, Set<Integer> set) {
        if (node == null) return;
        set.add(node.val);
        fill(node.left, set);
        fill(node.right, set);
    }
    boolean find(TreeNode node, Set<Integer> set, int target) {
        if (node == null) return false;
        if (set.contains(target - node.val)) return true;
        return find(node.left, set, target) || find(node.right, set, target);
    }
}
Python
def twoSumBSTs(root1, root2, target):
    def fill(node, s):
        if not node: return
        s.add(node.val)
        fill(node.left, s)
        fill(node.right, s)
    s = set()
    fill(root1, s)
    def find(node):
        if not node: return False
        if target - node.val in s: return True
        return find(node.left) or find(node.right)
    return find(root2)

Complexity

  • ⏰ Time complexity: O(n + m) — n, m = number of nodes in each tree.
  • 🧺 Space complexity: O(n) — For the set of values from one tree.

Comments