Problem

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

  • nums1[i] == nums2[j], and
  • the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

Examples

Example 1

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2019/04/26/142.png)

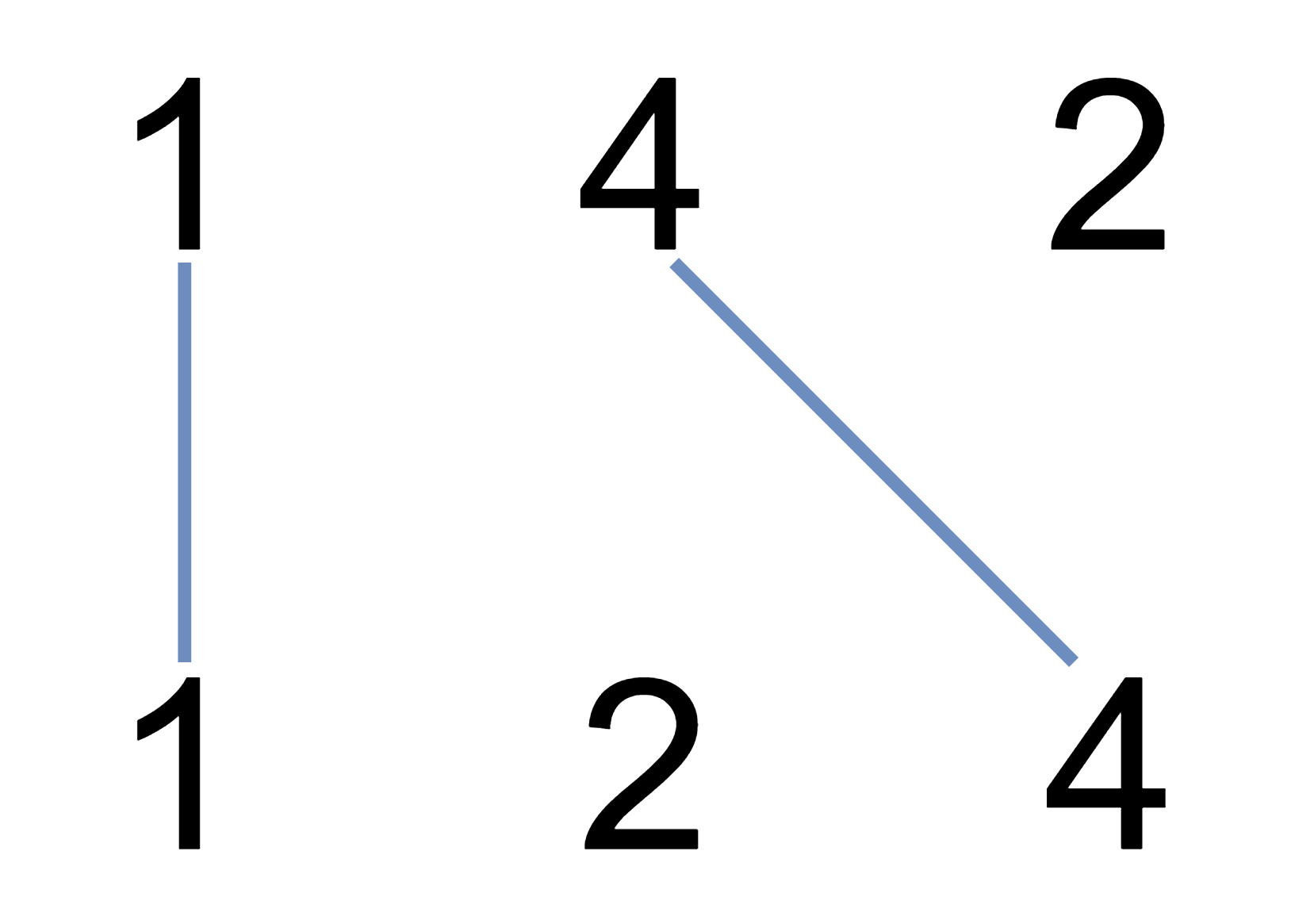
Input: nums1 = [1,4,2], nums2 = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

Example 2

1
2

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
Output: 3

Example 3

1
2

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
Output: 2

Constraints

  • 1 <= nums1.length, nums2.length <= 500
  • 1 <= nums1[i], nums2[j] <= 2000

Solution

Method 1 – Dynamic Programming (LCS)

Intuition

This is the same as finding the length of the longest common subsequence (LCS) between nums1 and nums2.

Approach

  1. Use a 2D DP array where dp[i][j] is the max number of lines for nums1[:i] and nums2[:j].
  2. If nums1[i-1] == nums2[j-1], dp[i][j] = dp[i-1][j-1] + 1.
  3. Else, dp[i][j] = max(dp[i-1][j], dp[i][j-1]).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int n = nums1.length, m = nums2.length;
        int[][] dp = new int[n+1][m+1];
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                if (nums1[i-1] == nums2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[n][m];
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def maxUncrossedLines(nums1, nums2):
    n, m = len(nums1), len(nums2)
    dp = [[0]*(m+1) for _ in range(n+1)]
    for i in range(1, n+1):
        for j in range(1, m+1):
            if nums1[i-1] == nums2[j-1]:
                dp[i][j] = dp[i-1][j-1] + 1
            else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])
    return dp[n][m]

Complexity

  • ⏰ Time complexity: O(n*m) — n = len(nums1), m = len(nums2).
  • 🧺 Space complexity: O(n*m) — For the DP table.