Unique Paths in Grid 1-2 - Get all paths moving right or down

Problem

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return all possible unique paths that the robot can take to reach the bottom-right corner.

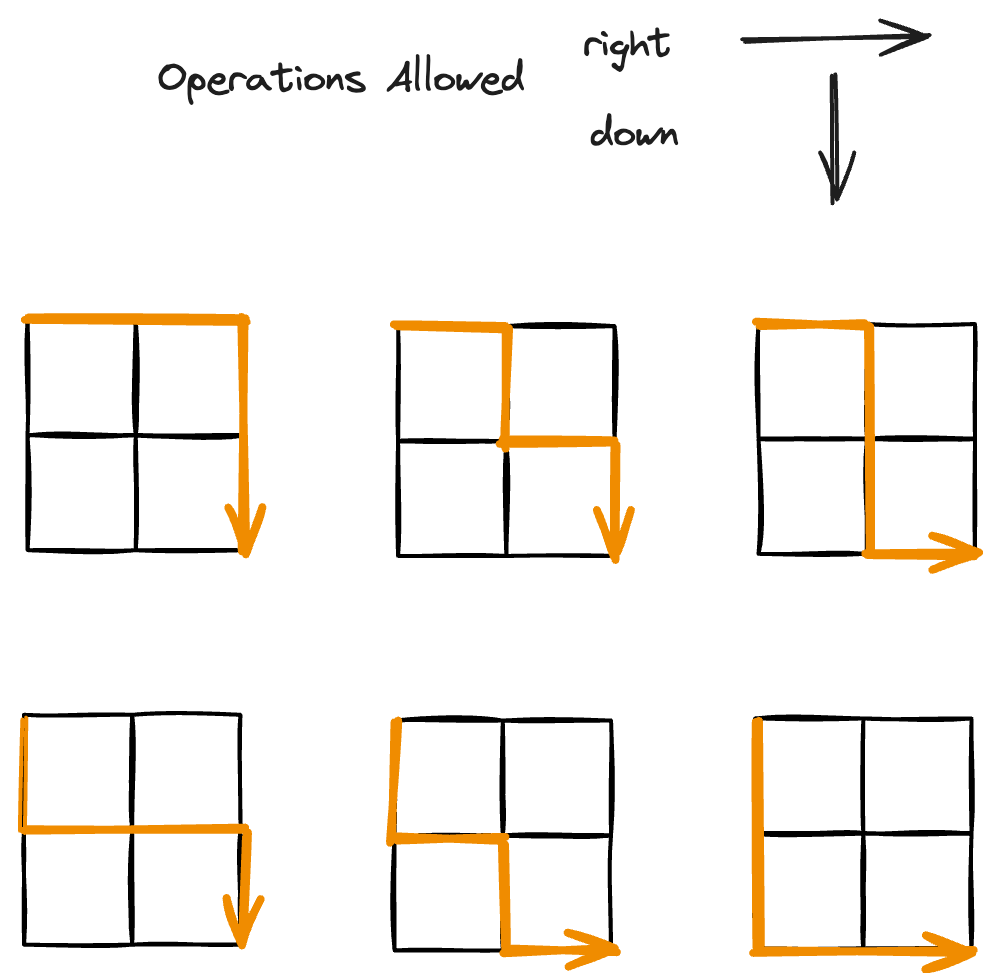
Examples

Example 1:

Input : m = 2, n = 2
Output : [ 
	[[0, 0], [0,1], [1,1]],
	[[0, 0], [1, 0], [1,1]]

2 possible routes : (0, 0) -> (0, 1) -> (1, 1)

Follow up

Imagine certain squares are “off limits”, such that the robot can not step on them. Design an algorithm to get all possible paths for the robot.

Refer [Unique Paths in Grid - Get all paths moving right or down with obstacles](unique-paths-in-grid-get-all-paths-moving-right-or-down-with-obstacles)

Solution

Method 1 - Backtracking

We solved the similar question - [Unique Paths in Grid 1 - Count all paths moving right or down](unique-paths-in-grid-1-count-all-paths-moving-right-or-down), where we had to find the count of number of paths. Here we have to print the paths.

Code

Java

public class Solution {

	public List < List<int[] >> findAllPaths(int m, int n) {
		List <List<int[]>> paths = new ArrayList<>();
		List <int[]> currentPath = new ArrayList<>();
		currentPath.add(new int[] {
			0, 0
		});
		backtrack(m, n, 0, 0, currentPath, paths);
		return paths;
	}

	private void backtrack(int m, int n, int row, int col, List <int[]> currentPath, List <List<int[]>> paths) {
		if (row == m - 1 && col == n - 1) {
			paths.add(new ArrayList<>(currentPath)); // Add a copy of the currentPath
			return;
		}

		// Move Down
		if (row < m - 1) {
			currentPath.add(new int[] {
				row + 1, col
			}); // Move down
			backtrack(m, n, row + 1, col, currentPath, paths);
			currentPath.remove(currentPath.size() - 1); // Backtrack
		}

		// Move Right
		if (col < n - 1) {
			currentPath.add(new int[] {
				row, col + 1
			}); // Move right
			backtrack(m, n, row, col + 1, currentPath, paths);
			currentPath.remove(currentPath.size() - 1); // Backtrack
		}
	}

	public static void main(String[] args) {
		Solution solution = new Solution();
		List < List<int[] >> paths = solution.findAllPaths(2, 3);

		// Print all paths
		for (List < int[] > path: paths) {
			System.out.print("[ ");

			for (int[] step: path) {
				System.out.print("[" + step[0] + "," + step[1] + "] ");
			}

			System.out.println("]");
		}
	}
}

Complexity

• ⏰ Time complexity: O(2 ^ (m+n))
• 🧺 Space complexity: O(m + n) for recursive stack