Unique Paths in Grid 1 - Count all paths moving right or down

Problem

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

There is a rat in a maze of size m x n, moving from top left corner to bottom right corner, moving only in two directions - down or right.

The test cases are generated so that the answer will be less than or equal to 2 * 10^9.

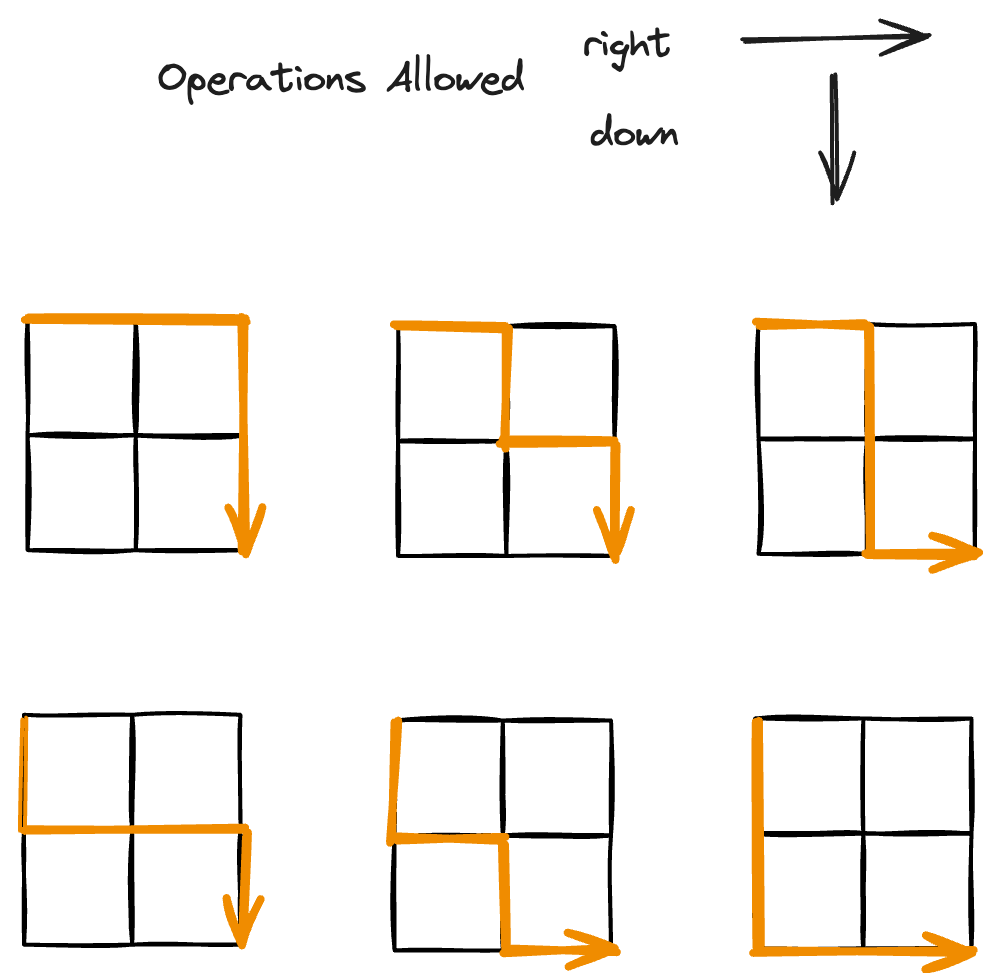
Note: m and n will be such that the resulting answer fits in a 32 bit signed integer.

Examples

Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3

Example 3:

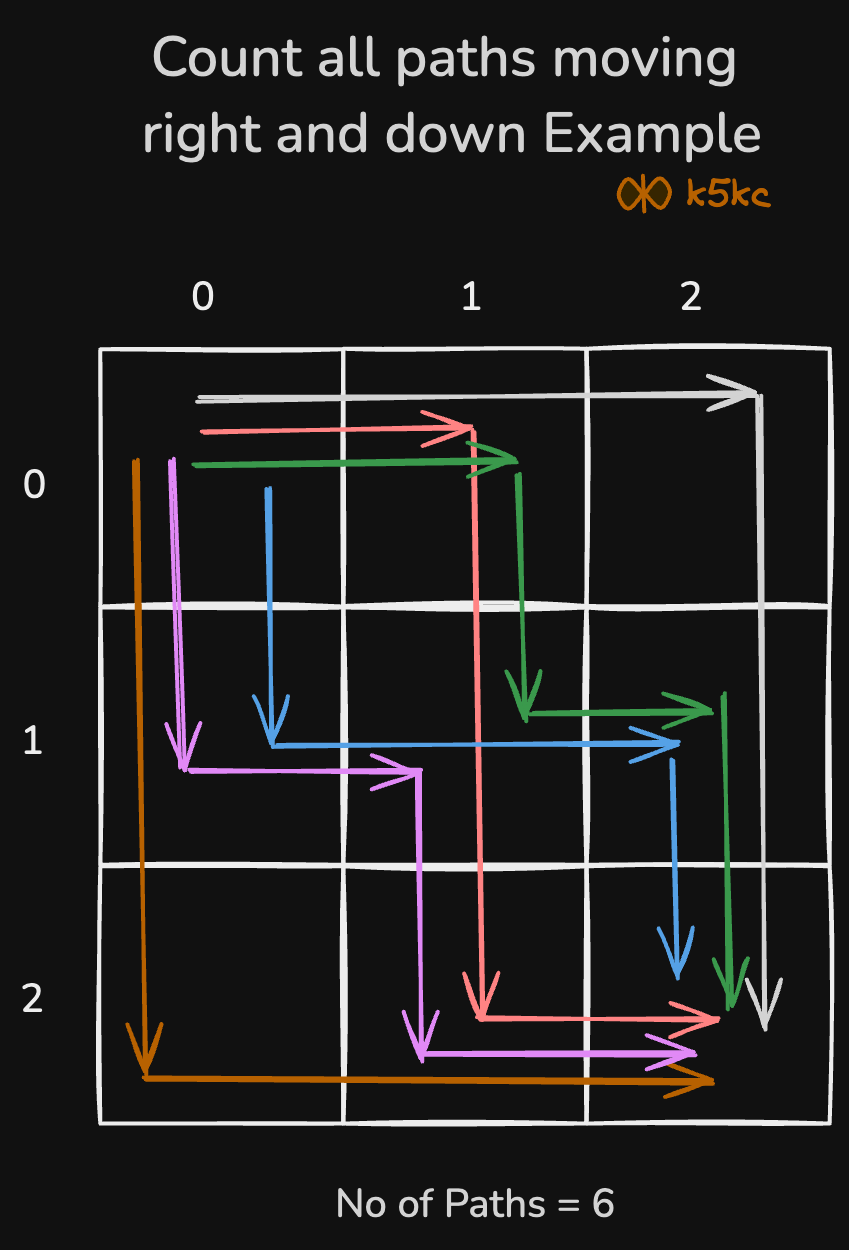
Input: m = 3, n = 3
Output: 6

Example 4:

Input : m = 2, n = 2
Output : 2

2 possible routes : (0, 0) -> (0, 1) -> (1, 1)
              OR  : (0, 0) -> (1, 0) -> (1, 1)

Solution

Video explanation

Here is the video explaining below methods in detail. Please check it out:

Method 1 - DFS and Recursion

Since we know that one can only move either down or right at any point in time

Base case: f(N, 0) = 1, f(0, N) = 1
Recursion: f(N, N) = f(N, N-1) + f(N-1, N)

Code

Java

Start from `0,0`

class Solution {

    public int uniquePaths(int m, int n) {
        return dfs(0, 0, m, n);
    }

    private int dfs(int i, int j, int m, int n) {
        // Base cases
        if (i >= m || j >= n) {
            return 0; // Out of bounds
        }
        if (i == m - 1 && j == n - 1) {
            return 1; // Reached the destination
        }

        // Recursive calls for moving down and right
        return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
    }
}

Check if end

We can also start from end destination, and shift our destination:

public int allPossiblePaths(int m, int n) {
	if (m == 0 || n == 0)
		return 1;
	return allPossiblePaths(m - 1, n) + allPossiblePaths(m, n - 1);
}

Python

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        def dfs(i: int, j: int) -> int:
            # Base cases
            if i >= m or j >= n:  # Out of bounds
                return 0
            if i == m - 1 and j == n - 1:  # Reached the destination
                return 1
            
            # Recursive calls for moving down and right
            return dfs(i + 1, j) + dfs(i, j + 1)
        
        return dfs(0, 0)  # Start from the top-left corner

Complexity

⏰ Time complexity: O(2^(m + n))
🧺 Space complexity: O(m + n)

Method 2 - Top Down DP with Memoization

We have a lot of repetition in Method 1, so we can use cache.

Code

Java

class Solution {
    public int uniquePaths(int m, int n) {
        // Initialise a DP table with -1 for caching
        int[][] memo = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                memo[i][j] = -1; // Mark all cells as unvisited
            }
        }
        return dfs(0, 0, m, n, memo);
    }

    private int dfs(int i, int j, int m, int n, int[][] memo) {
        // Base cases
        if (i >= m || j >= n) {
            return 0; // Out of bounds
        }
        if (i == m - 1 && j == n - 1) {
            return 1; // Destination reached
        }
        
        // If the result is already computed, return it
        if (memo[i][j] != -1) {
            return memo[i][j];
        }

        // Compute result recursively and store it in DP table
        memo[i][j] = dfs(i + 1, j, m, n, memo) + dfs(i, j + 1, m, n, memo);
        return memo[i][j];
    }
}

Python

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # Initialise a DP table with -1 for caching
        memo = [[-1 for _ in range(n)] for _ in range(m)]

        def dfs(i: int, j: int) -> int:
            # Base cases
            if i >= m or j >= n:  # Out of bounds
                return 0
            if i == m - 1 and j == n - 1:  # Destination reached
                return 1
            
            # If the result is already computed, return it
            if memo[i][j] != -1:
                return memo[i][j]
            
            # Compute result recursively and store it in DP table
            memo[i][j] = dfs(i + 1, j) + dfs(i, j + 1)
            return memo[i][j]
        
        # Start DFS from the top-left corner
        return dfs(0, 0)

Complexity

⏰ Time complexity: O(m*n) as with caching, as each cell (i, j) is visited only once.
🧺 Space complexity: O(m*n)
- The cache occupies space proportional to the size of the grid (i.e., O(m * n)).
- While recursion still uses stack space of O(m + n), the reduced number of calls prevents excessive stack depth compared to the naive approach.

Method 3 - Bottom up DP

We can start filling numbers of ways we can reach to point [i,j] from [0,0]. For the first row, we can just reach in one way, from left to right. Likewise, for the first column, we can reach in 1 way, i.e. top to bottom. For the 4X5 matrix:

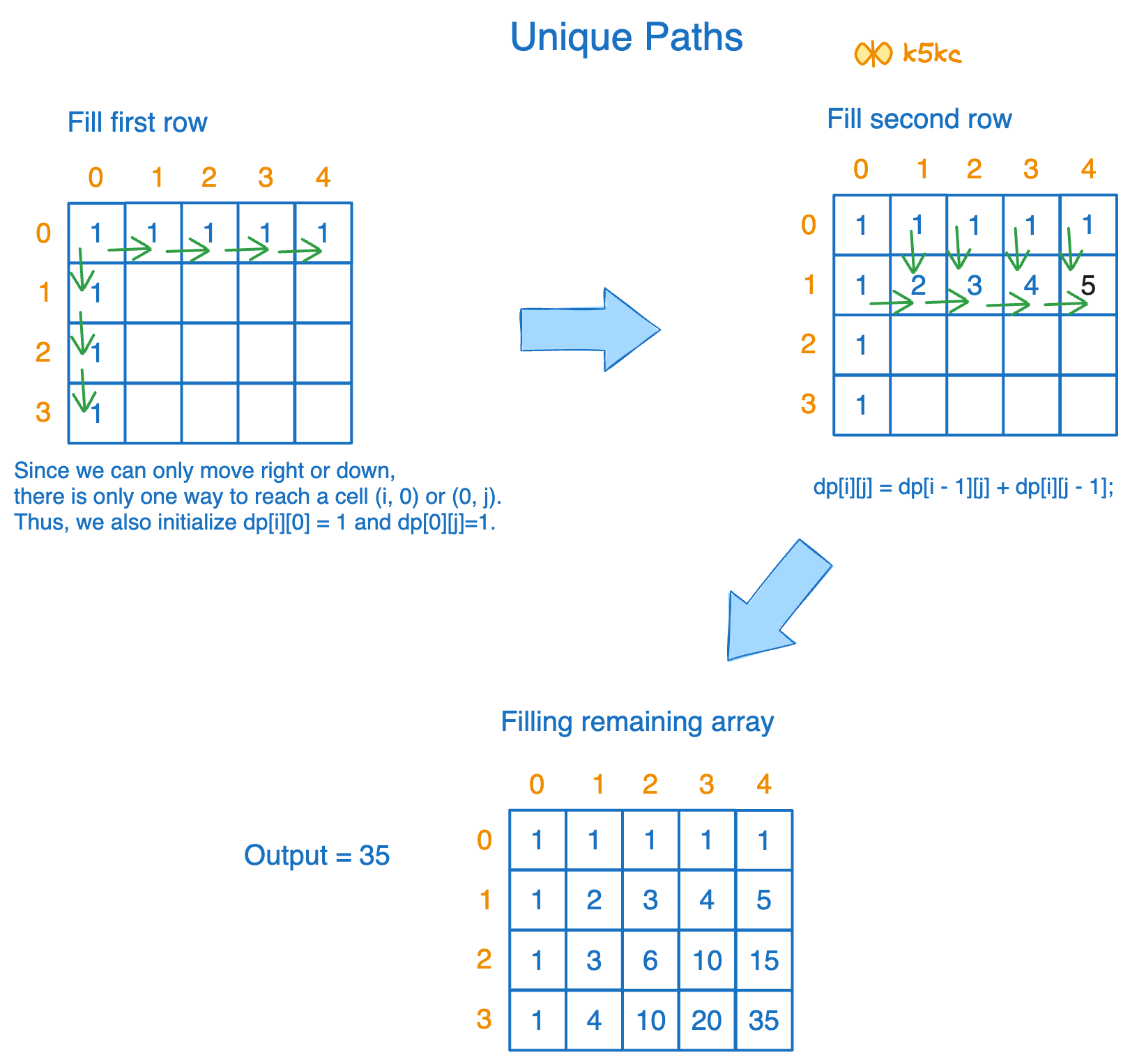
Now, that we have the base case, we can start filling further. Now we will start filling row wise. For eg. For first row, we can either come from left or top, hence 2 ways. Likewise, we can fill remaining row. Total:

dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

Code

Java

class Solution {
    public int uniquePaths(int m, int n) {
        // Create a DP table with dimensions m x n
        int[][] dp = new int[m][n];

        // Initialise the first row and first column to 1
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = 1;
        }

        // Fill the DP table from top-left to bottom-right
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1]; // Sum of top and left cells
            }
        }

        // Return the result at the bottom-right corner
        return dp[m-1][n-1];
    }
}

Python

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # Create a DP table with dimensions m x n
        dp = [[0 for _ in range(n)] for _ in range(m)]

        # Initialise the first row and first column to 1
        for i in range(m):
            dp[i][0] = 1
        for j in range(n):
            dp[0][j] = 1

        # Fill the DP table from top-left to bottom-right
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]  # Sum of top and left cells

        # Return the result at the bottom-right corner
        return dp[m-1][n-1]

Complexity

⏰ Time complexity: O(m * n) as filling the m x n grid iteratively involves a single computation per cell.
🧺 Space complexity: O(m * n) as the DP table requires space proportional to the size of the grid.

Method 4 - Space efficient DP

While the bottom-up DP approach with a full m x n grid works well, it uses O(m * n) space for storing the paths for all cells. However, if we closely observe the problem, we only need the values of the current row (or column) and the previous row (or column) at any given time to compute the solution for the next row or column.

This insight allows us to reduce the space usage significantly by storing only one row or column at any time instead of the entire grid. Using this optimisation, the space complexity can be reduced from O(m * n) to O(\min(m, n)), depending on whether we iterate row-wise or column-wise.

Code

Java

class Solution {
    public int uniquePaths(int m, int n) {
        // Ensure we're iterating over the smaller dimension for reduced memory usage
        if (m < n) {
            int temp = m;
            m = n;
            n = temp;
        }

        // Use a 1D array to represent the paths for a single row or column
        int[] dp = new int[n];
        for (int j = 0; j < n; j++) {
            dp[j] = 1; // Initialise the first row to 1
        }

        // Iterate through the grid, updating paths row by row
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[j] += dp[j-1]; // Update current cell as sum of left and above cells
            }
        }

        // The result is stored in the last cell of the array
        return dp[n-1];
    }
}

Python

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # Use a single row array to represent the current state
        if m < n:
            m, n = n, m  # Ensure we are using the smaller dimension for the array (n)

        # Initialise a 1D array for the current row (represents the paths for a single row)
        dp = [1] * n

        # Iterate through the grid row by row
        for i in range(1, m):
            for j in range(1, n):
                dp[j] += dp[j-1]  # Update current cell as sum of the left and top cells

        # The last cell in the array contains the result (bottom-right corner)
        return dp[-1]

Complexity

⏰ Time complexity: O(m * n)
🧺 Space complexity: O(min(m, n))

Method 5 - Combinatorics

This problem can be modelled as a math combinatorics problem.

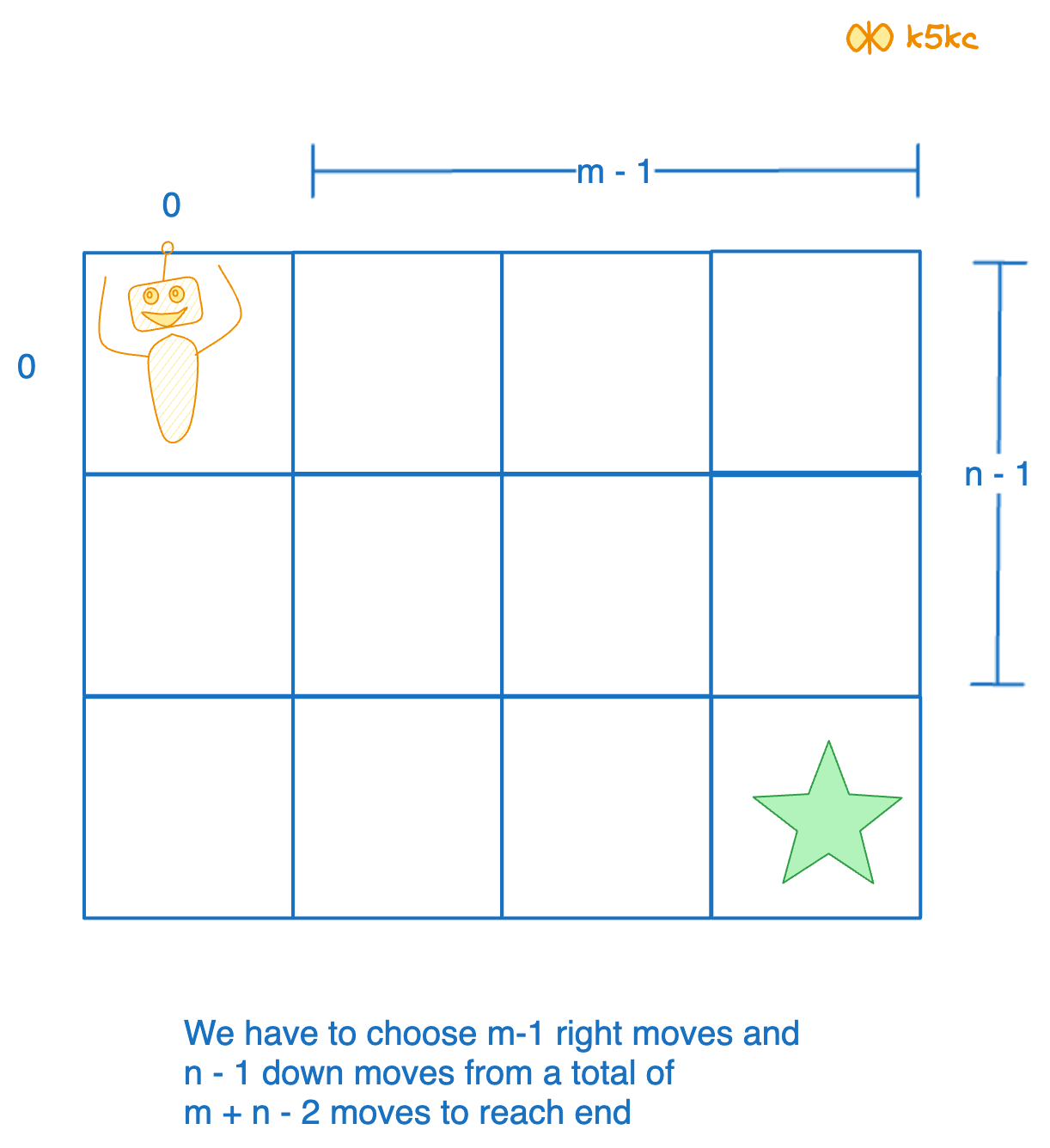
We start at (0, 0) cell and end at (m-1, n-1) cell.
We have to make m-1 down-moves and n-1 right-moves to reach the destination cell.
Hence, we need to perform a total number of m+n-2 moves.
At each cell along the path, we can choose either the right-move or down-move and we need to find the number of unique combinations of these choices (which eventually leads to unique paths).
This is nothing but calculating the number of different ways to choose m-1 down-moves and n-1 right-moves from a total of m+n-2 moves.

Hence we have to calculate:

\text{Number of moves} = \binom{m + n - 2}{m - 1} OR \binom{m + n - 2}{n - 1}

we can use [Binomial Coefficient](calculate-the-binomial-coefficient) to do so. Or we can solve the relation below:

\binom{m + n - 2}{m - 1} = \binom{m + n - 2}{n - 1} = \frac{(m + n - 2)!}{(m - 1)!(n-1)!}

\implies \binom{m + n - 2}{m - 1} = \frac{(m + n - 2) * (m + n - 3) * ... * (m + n - n) * (m - 1)!}{(m - 1)!(n-1)!}

\implies = \frac{(m + n - 2) * (m + n - 3) * ... * m}{(n-1)!}

\implies = \frac{(m + n - 2) * (m + n - 3) * ... * m}{(n-1) * (n - 2) ... * 2 * 1}

We could have cancelled out the (n-1)! as well in the above evaluation, but we will do one of those based on min(m,n) to give best time complexity in the solution below.

Code

Java

public class Solution {

	public int uniquePaths(int m, int n) {
		long ans = 1;

		for (int i = m + n - 2, j = 1; i >= Math.max(m, n); i--, j++) {
			ans = (ans * i) / j;
		}

		return (int) ans;
	}
}

Python

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # Calculate the number of unique paths using combination formula
        return comb(m + n - 2, n - 1)

Complexity

⏰ Time complexity: O(min(m, n)). This is because we compute factorials for m-1, n-1, and m+n-2, where the smaller number determines the computational intensity.
🧺 Space complexity: O(1) as this approach does not use additional data structures or recursion, as it simply performs arithmetic operations on integers.

Problem

Examples

Solution

Video explanation

Method 1 - DFS and Recursion

Code

Java

Start from 0,0

Check if end

Python

Complexity

Method 2 - Top Down DP with Memoization

Code

Java

Python

Complexity

Method 3 - Bottom up DP

Code

Java

Python

Complexity

Method 4 - Space efficient DP

Code

Java

Python

Complexity

Method 5 - Combinatorics

Code

Java

Python

Complexity

Comments

Start from `0,0`