Problem

You are given an m x n integer array grid where grid[i][j] could be:

  • 1 representing the starting square. There is exactly one starting square.
  • 2 representing the ending square. There is exactly one ending square.
  • 0 representing empty squares we can walk over.
  • -1 representing obstacles that we cannot walk over.

Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.

Examples

Example 1:

1
2
3
4
5
6
7

Input:
grid =[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
Output:
 2
Explanation: We have the following two paths: 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

Example 2:

1
2
3
4
5
6
7
8
9

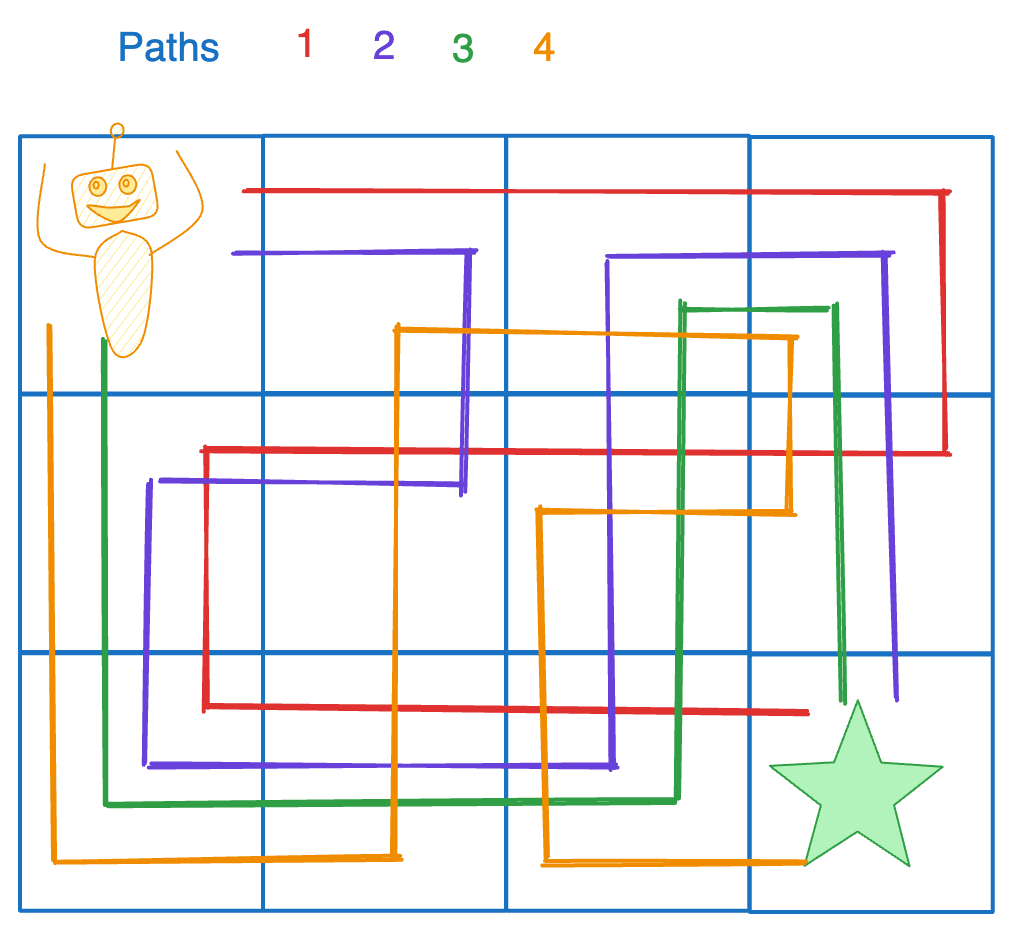
Input:
grid =[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
Output:
 4
Explanation: We have the following four paths: 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

Example 3:

1
2
3
4
5
6

Input:
grid =[[0,1],[2,0]]
Output:
 0
Explanation: There is no path that walks over every empty square exactly once.
Note that the starting and ending square can be anywhere in the grid.

Solution

Method 1 - Backtracking with array modification and restoration

Here is the algo we can follow:

  • First find out where to start (We dont need to find end yet, but we can do it while DFS)
  • Also We need to know the number of empty cells, say numEmpty.

Then we start our dfs from start such that our steps become equal tonumEmpty. We we try to explore a cell, it will change 0 to -1 (or some negative number) and do a dfs in 4 direction. (Another approach is is to use visited set)

If we hit the target and pass all empty cells, increment the result.

Why Are We Setting numEmpty = 1 to Begin With?

That is to count the start element. Where we start from is kind of an empty place. Think about the situation of only two elements like [[1,2]], you will understand.

Blocking with -2

We can also set grid[i][j] = -2 and restore it to 0. To differentiate at any time if we blocked the place for DFS. Then we have to change the condition:

1
2
3

if (i < 0 || i == grid.length || j < 0 || j == grid[0].length || grid[i][j] == -1) {
		return 0;
}

To

1
2
3

if (i < 0 || i == grid.length || j < 0 || j == grid[0].length || grid[i][j] < 0) {
		return 0;
}

Here is our DFS looks

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class Solution {

	public int uniquePathsIII(int[][] grid) {
		int sx = 0, sy = 0, numEmpty = 1; // starting x and y, number of empty cells
		for (int i = 0; i < grid.length; i++) {
			for (int j = 0; j < grid[0].length; j++) {
				if (grid[i][j] == 0) {
					numEmpty++;
				} else if (grid[i][j] == 1) {
					sx = i;
					sy = j;
				}
			}
		}

		// start dfs with start position
		return dfs(grid, sx, sy, 0, numEmpty);
	}

	private int dfs(int[][] grid, int i, int j, int count, int need) {
		if (i < 0 || i == grid.length || j < 0 || j == grid[0].length || grid[i][j] == -1) {
			return 0;
		}

		if (grid[i][j] == 2) {
			if (count == need) {
				return 1;
			} else {
				return 0;
			}
		}

		grid[i][j] = -1; // convert open space to blocked
		int total = dfs(grid, i - 1, j, count + 1, need);
		total += dfs(grid, i, j + 1, count + 1, need);
		total += dfs(grid, i + 1, j, count + 1, need);
		total += dfs(grid, i, j - 1, count + 1, need);
		grid[i][j] = 0; // backtrack

		return total;
	}
}

Complexity

  • ⏰ Time complexity: O(4^(m*n), where m is the number of rows and n is the number of columns in grid. This is the worst-case scenario where nearly all cells are empty, and at each step, there are 4 different directions that can be chosen (up, down, left, right).
  • 🧺 Space complexity: O(m*n) - considering recursion stack, but O(1) if we don’t consider it assuming array modification.

Method 2 - Backtracking With Visited Set

Here is the same with visited set.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

class Solution {

	public int uniquePathsIII(int[][] grid) {
		int empty = 0;
		int m = grid.length, n = grid[0].length, sx = 0, sy = 0;

		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				if (grid[i][j] == 0) empty++;
				else if (grid[i][j] == 1) {
					sx = i;
					sy = j;
				}
			}
		}

		return dfs(grid, sx, sy, new boolean[m][n]);
	}

	private int dfs(int[][] grid, int x, int y, int empty, boolean[][] visited) {
		if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] == -1 || visited[x][y]) {
			return 0;
		}

		if (grid[x][y] == 2) {
			if (empty == 0) {
				return 1;
			} else {
				return 0; // terminate early
			}
		}

		int ans = 0;
		visited[x][y] = true;

		if (grid[x][y] == 0) empty--;
		ans += dfs(grid, x + 1, y, empty, visited);
		ans += dfs(grid, x - 1, y, empty, visited);
		ans += dfs(grid, x, y + 1, empty, visited);
		ans += dfs(grid, x, y - 1, empty, visited);
		visited[x][y] = false;

		if (grid[x][y] == 0) empty++;

		return ans;
	}
}