Unique Paths in Grid - Get all paths moving right or down with obstacles

Problem

You are given an m x n integer array grid. There is a robot initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m-1][n-1]). The robot can only move either down or right at any point in time.

An obstacle and space are marked as 1 or 0 respectively in grid. A path that the robot takes cannot include any square that is an obstacle.

Return all possible unique paths that the robot can take to reach the bottom-right corner.

Examples

Example 1:

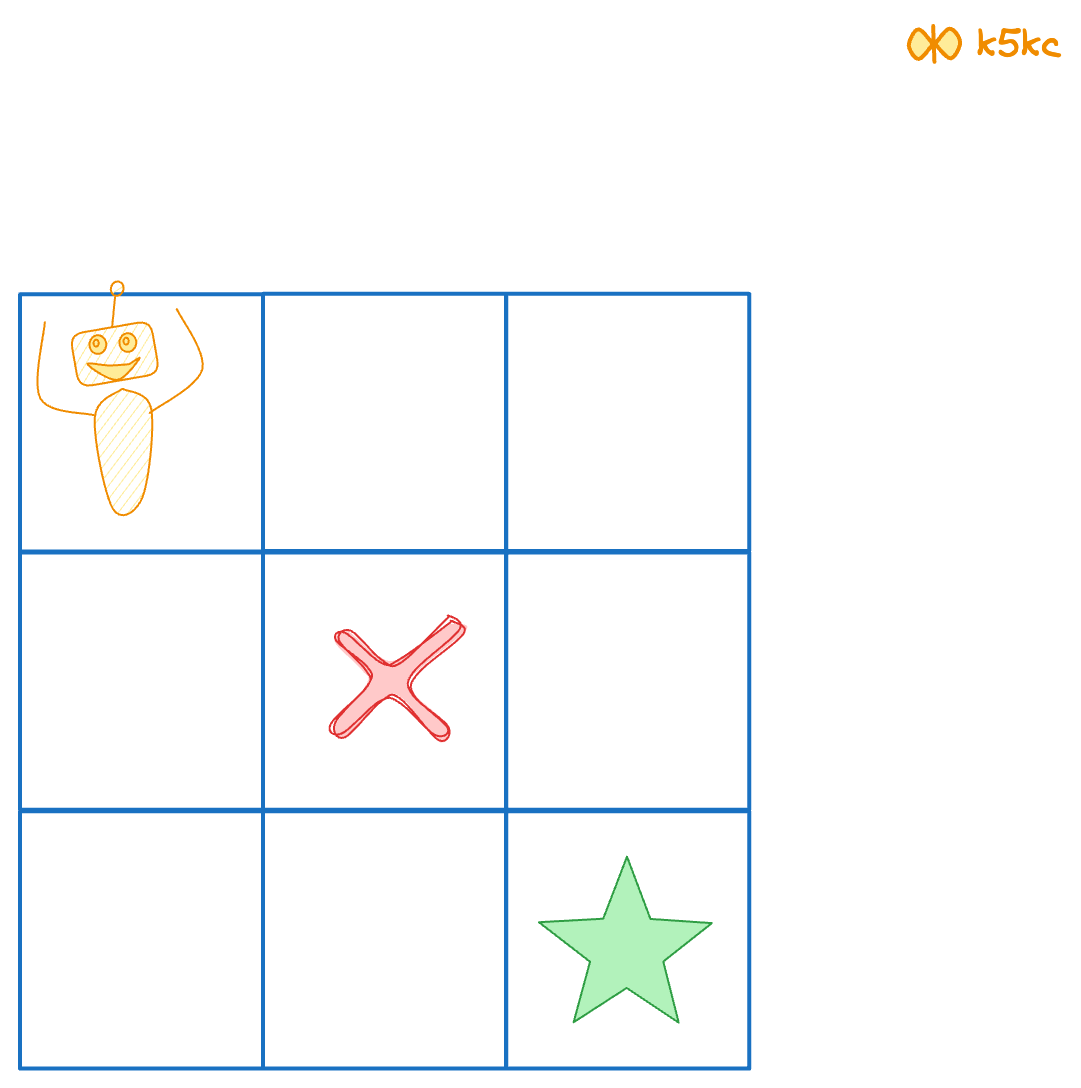
There is one obstacle in the middle of a 3x3 grid as illustrated below.

Input:
obstacleGrid =[[0,0,0],[0,1,0],[0,0,0]]
Output:
 [ 
	[[0, 0], [0, 1], [0, 2], [1, 2], [2, 2]],
	[[0, 0], [1, 0], [2, 0], [2, 1], [2, 2]]
 ]
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Example 2:

Input:
obstacleGrid =[[0,1],[0,0]]
Output:
 [ 
	[[0, 0], [1, 0], [1, 1]]
 ]

Note: m and n will be at most 100.

Follow-up

What if you need to return any valid path? (Answered inside Method 1.)

Solution

Method 1 - Backtracking Enumeration (All Paths)

Intuition

Every valid path from top-left to bottom-right using only Right and Down steps (and avoiding obstacles) can be represented as a sequence of at most (m + n - 2) decisions. A depth-first traversal that tries both allowed directions from each cell will enumerate all such paths. Because movement is monotonic (never up/left), no cycles occur, so we do not need a visited matrix—each path prefix is unique in the search tree.

Approach

1. Start DFS from (0, 0); maintain a current path list.
2. If current cell is out of bounds or an obstacle (1), return.
3. Append current cell to path.
4. If destination reached, copy path to results.
5. Recurse (Down, then Right or any fixed order) and backtrack by removing the cell.

Code

Java

public class Solution {
	public List<List<int[]>> enumerateAllPaths(int[][] grid) {
		List<List<int[]>> res = new ArrayList<>();
		int m = grid.length, n = grid[0].length;
		if (grid[0][0] == 1 || grid[m-1][n-1] == 1) return res;
		dfs(grid, 0, 0, new ArrayList<>(), res);
		return res;
	}

	private void dfs(int[][] g, int r, int c, List<int[]> cur, List<List<int[]>> res) {
		int m = g.length, n = g[0].length;
		if (r < 0 || c < 0 || r >= m || c >= n || g[r][c] == 1) return;
		cur.add(new int[]{r,c});
		if (r == m - 1 && c == n - 1) {
			res.add(new ArrayList<>(cur));
		} else {
			dfs(g, r + 1, c, cur, res); // Down
			dfs(g, r, c + 1, cur, res); // Right
		}
		cur.remove(cur.size()-1);
	}
}

Python

from typing import List, Tuple

class Solution:
    def enumerateAllPaths(self, grid: List[List[int]]) -> List[List[Tuple[int,int]]]:
        """Enumerate all valid Right/Down obstacle-avoiding paths."""
        m, n = len(grid), len(grid[0])
        if grid[0][0] == 1 or grid[m-1][n-1] == 1:
            return []
        res: List[List[Tuple[int,int]]] = []
        path: List[Tuple[int,int]] = []

        def dfs(r: int, c: int) -> None:
            if r < 0 or c < 0 or r >= m or c >= n or grid[r][c] == 1:
                return
            path.append((r, c))
            if r == m - 1 and c == n - 1:
                res.append(path.copy())
            else:
                dfs(r + 1, c)   # Down
                dfs(r, c + 1)   # Right
            path.pop()

        dfs(0, 0)
        return res

if __name__ == "__main__":
    g = [[0,0,0],[0,1,0],[0,0,0]]
    sol = Solution()
    print("All:", sol.enumerateAllPaths(g))
    print("One:", sol.findAnyPath(g))

Complexity

• ⏰ Time complexity: O(P * (m + n)) – enumerating all paths visits each valid path (length ≈ m + n) once; worst-case without obstacles P = C(m + n - 2, m - 1) (combinatorial / exponential in m + n).
• 🧺 Space complexity: O(m + n) – recursion depth equals path length; result storage for all paths is output size Θ(P * (m + n)) (excluded from complexity bound by convention).

Solution - Follow up - Return any path

Method 1 - Backtracking again

If you only need a single valid path, introduce a found flag (or return boolean) and stop recursing once the destination is found. This prunes the remaining exponential branches. Worst-case still explores many nodes if the successful path is “last”, but in practice on average grids the early-exit version is much faster. For a guaranteed polynomial approach regardless of branching, a DP reachability + parent reconstruction method (not shown here) runs in O(m * n).

Code

Java

public class Solution {
	// Follow-up variant: return any one path; stops early once found.
	public List<int[]> findAnyPath(int[][] grid) {
		List<int[]> path = new ArrayList<>();
		if (grid[0][0] == 1 || grid[grid.length-1][grid[0].length-1] == 1) return path;
		dfsOne(grid, 0, 0, path);
		return path;
	}

	private boolean dfsOne(int[][] g, int r, int c, List<int[]> path) {
		int m = g.length, n = g[0].length;
		if (r < 0 || c < 0 || r >= m || c >= n || g[r][c] == 1) return false;
		path.add(new int[]{r,c});
		if (r == m - 1 && c == n - 1) return true;
		if (dfsOne(g, r, c + 1, path) || dfsOne(g, r + 1, c, path)) return true; // try Right then Down
		path.remove(path.size()-1); // backtrack
		return false;
	}

	public static void main(String[] args) {
		int[][] grid = {{0,0,0},{0,1,0},{0,0,0}};
		Solution s = new Solution();
		List<List<int[]>> all = s.enumerateAllPaths(grid);
		System.out.println("All paths:");
		for (List<int[]> p : all) System.out.println(p.stream().map(a->"["+a[0]+","+a[1]+"]").toList());
		System.out.println("Any one path:");
		List<int[]> one = s.findAnyPath(grid);
		System.out.println(one.stream().map(a->"["+a[0]+","+a[1]+"]").toList());
	}
}

Python

from typing import List, Tuple

class Solution:

    def findAnyPath(self, grid: List[List[int]]) -> List[Tuple[int,int]]:
        """Return any one valid path using early-exit backtracking; [] if none."""
        m, n = len(grid), len(grid[0])
        if grid[0][0] == 1 or grid[m-1][n-1] == 1:
            return []
        path: List[Tuple[int,int]] = []
        found = False

        def dfs(r: int, c: int) -> bool:
            nonlocal found
            if r < 0 or c < 0 or r >= m or c >= n or grid[r][c] == 1 or found:
                return False
            path.append((r, c))
            if r == m - 1 and c == n - 1:
                found = True
                return True
            # Try Right then Down (order arbitrary)
            if dfs(r, c + 1) or dfs(r + 1, c):
                return True
            path.pop()
            return False

        dfs(0, 0)
        return path if found else []

if __name__ == "__main__":
    g = [[0,0,0],[0,1,0],[0,0,0]]
    sol = Solution()
    print("All:", sol.enumerateAllPaths(g))
    print("One:", sol.findAnyPath(g))

Complexity

• ⏰ Time complexity: O(m + n) The single-path early-exit variant is between O(m + n) (first path succeeds immediately) and the same exponential bound in the worst case.
• 🧺 Space complexity: O(1) Single-path variant only stores one path.