problemmediumalgorithmsleetcode-3528leetcode 3528leetcode3528

Unit Conversion I

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There are n types of units indexed from 0 to n - 1. You are given a 2D integer array conversions of length n - 1, where conversions[i] = [sourceUniti, targetUniti, conversionFactori]. This indicates that a single unit of type sourceUniti is equivalent to conversionFactori units of type targetUniti.

Return an array baseUnitConversion of length n, where baseUnitConversion[i] is the number of units of type i equivalent to a single unit of type 0. Since the answer may be large, return each baseUnitConversion[i] modulo 10^9 + 7.

Examples

Example 1

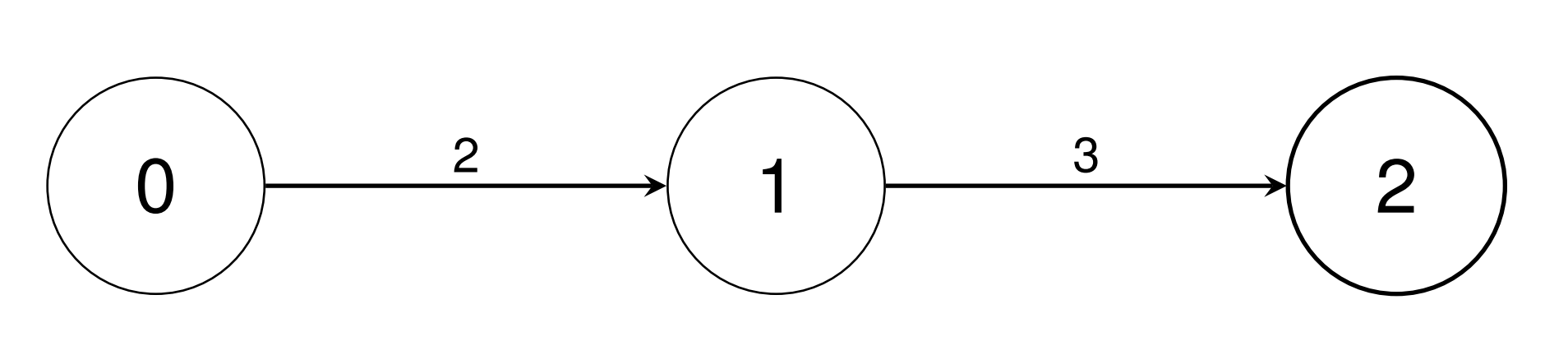
Input: conversions = [[0,1,2],[1,2,3]]
Output: [1,2,6]
Explanation:
* Convert a single unit of type 0 into 2 units of type 1 using `conversions[0]`.
* Convert a single unit of type 0 into 6 units of type 2 using `conversions[0]`, then `conversions[1]`.
![](https://assets.leetcode.com/uploads/2025/03/12/example1.png)

Example 2

Input: conversions =
[[0,1,2],[0,2,3],[1,3,4],[1,4,5],[2,5,2],[4,6,3],[5,7,4]]
Output: [1,2,3,8,10,6,30,24]
Explanation:
* Convert a single unit of type 0 into 2 units of type 1 using `conversions[0]`.
* Convert a single unit of type 0 into 3 units of type 2 using `conversions[1]`.
* Convert a single unit of type 0 into 8 units of type 3 using `conversions[0]`, then `conversions[2]`.
* Convert a single unit of type 0 into 10 units of type 4 using `conversions[0]`, then `conversions[3]`.
* Convert a single unit of type 0 into 6 units of type 5 using `conversions[1]`, then `conversions[4]`.
* Convert a single unit of type 0 into 30 units of type 6 using `conversions[0]`, `conversions[3]`, then `conversions[5]`.
* Convert a single unit of type 0 into 24 units of type 7 using `conversions[1]`, `conversions[4]`, then `conversions[6]`.

Constraints

  • 2 <= n <= 10^5
  • conversions.length == n - 1
  • 0 <= sourceUniti, targetUniti < n
  • 1 <= conversionFactori <= 10^9
  • It is guaranteed that unit 0 can be converted into any other unit through a unique combination of conversions without using any conversions in the opposite direction.

Solution

Method 1 – DFS/BFS for Conversion Multipliers

Intuition

The conversions form a directed tree rooted at unit 0. We can traverse the tree and compute the conversion multiplier for each unit from unit 0.

Approach

  1. Build a directed graph from the conversions.
  2. Use DFS or BFS to compute the multiplier for each unit from unit 0.
  3. Store the result modulo 1e9+7.

Code

C++
#include <vector>
#define MOD 1000000007
using namespace std;
vector<int> baseUnitConversion(int n, vector<vector<int>>& conversions) {
    vector<vector<pair<int, int>>> g(n);
    for (auto& c : conversions) {
        g[c[0]].emplace_back(c[1], c[2]);
    }
    vector<long long> res(n, 1);
    function<void(int)> dfs = [&](int u) {
        for (auto& [v, f] : g[u]) {
            res[v] = res[u] * f % MOD;
            dfs(v);
        }
    };
    dfs(0);
    vector<int> ans(n);
    for (int i = 0; i < n; ++i) ans[i] = res[i];
    return ans;
}
Java
import java.util.*;
class Solution {
    static final int MOD = 1_000_000_007;
    public int[] baseUnitConversion(int n, int[][] conversions) {
        List<List<int[]>> g = new ArrayList<>();
        for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
        for (int[] c : conversions) g.get(c[0]).add(new int[]{c[1], c[2]});
        long[] res = new long[n];
        Arrays.fill(res, 1);
        dfs(0, g, res);
        int[] ans = new int[n];
        for (int i = 0; i < n; ++i) ans[i] = (int)res[i];
        return ans;
    }
    void dfs(int u, List<List<int[]>> g, long[] res) {
        for (int[] e : g.get(u)) {
            int v = e[0], f = e[1];
            res[v] = res[u] * f % MOD;
            dfs(v, g, res);
        }
    }
}
Python
def baseUnitConversion(n, conversions):
    from collections import defaultdict
    MOD = 10**9 + 7
    g = defaultdict(list)
    for u, v, f in conversions:
        g[u].append((v, f))
    res = [1] * n
    def dfs(u):
        for v, f in g[u]:
            res[v] = res[u] * f % MOD
            dfs(v)
    dfs(0)
    return res

Complexity

  • ⏰ Time complexity: O(n) — Each node is visited once.
  • 🧺 Space complexity: O(n) — For graph and result array.

Comments