Problem

There are n types of units indexed from 0 to n - 1.

You are given a 2D integer array conversions of length n - 1, where conversions[i] = [sourceUniti, targetUniti, conversionFactori]. This indicates that a single unit of type sourceUniti is equivalent to conversionFactori units of type targetUniti.

You are also given a 2D integer array queries of length q, where queries[i] = [unitAi, unitBi].

Return an array answer of length q where answer[i] is the number of units of type unitBi equivalent to 1 unit of type unitAi, and can be represented as p/q where p and q are coprime. Return each answer[i] as pq-1 modulo 109 + 7, where q-1 represents the multiplicative inverse of q modulo 10^9 + 7.

Examples

Example 1

1
2
3
4
5

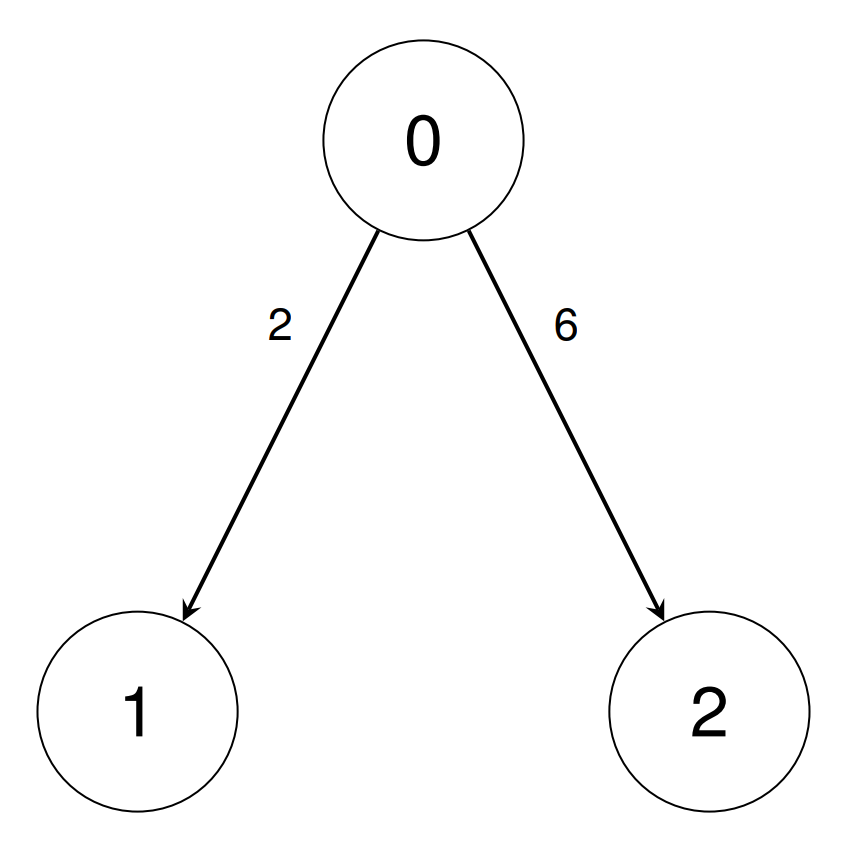
Input: conversions = [[0,1,2],[0,2,6]], queries = [[1,2],[1,0]]
Output: [3,500000004]
Explanation:
In the first query, we can convert unit 1 into 3 units of type 2 using the inverse of conversions[0], then conversions[1].
In the second query, we can convert unit 1 into 1/2 units of type 0 using the inverse of conversions[0]. We return 500000004 since it is the multiplicative inverse of 2.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

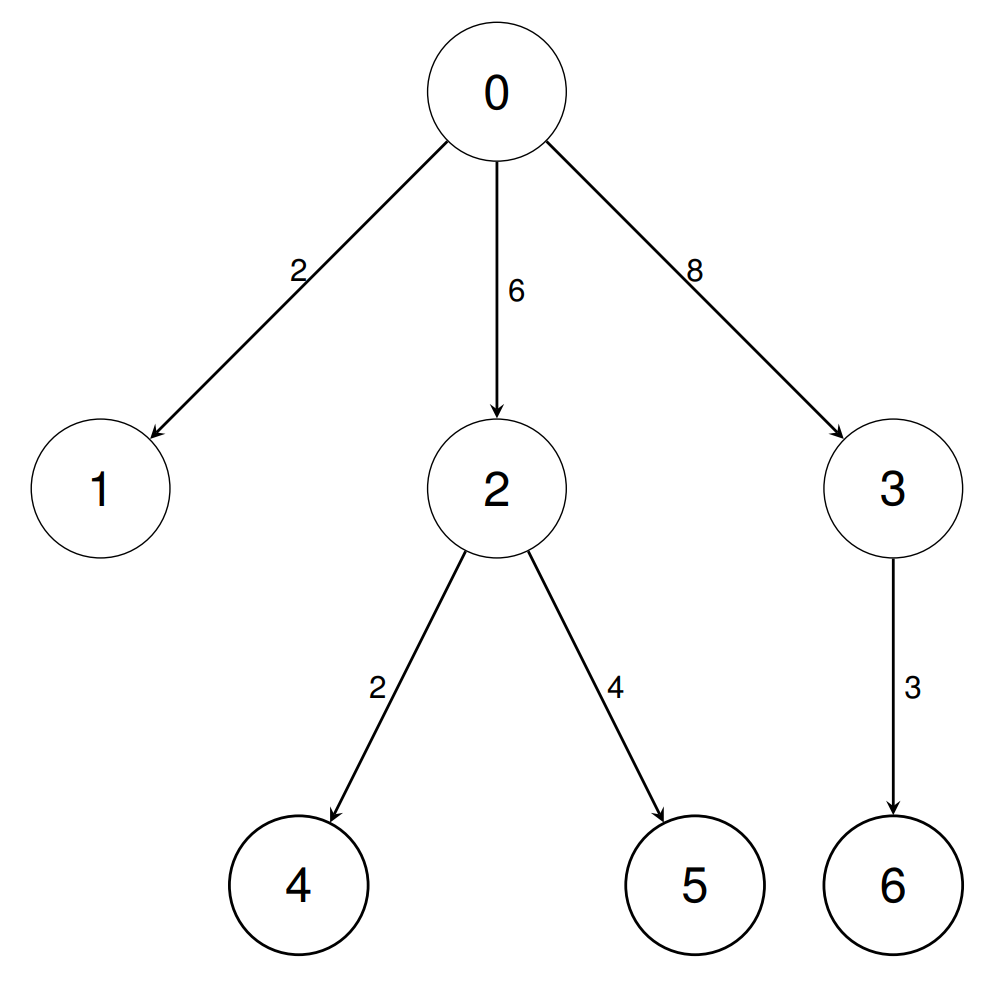
Input: conversions = [[0,1,2],[0,2,6],[0,3,8],[2,4,2],[2,5,4],[3,6,3]], queries = [[1,2],[0,4],[6,5],[4,6],[6,1]]

Output: [3,12,1,2,83333334]

Explanation:

In the first query, we can convert unit 1 into 3 units of type 2 using the inverse of conversions[0], then conversions[1].
In the second query, we can convert unit 0 into 12 units of type 4 using conversions[1], then conversions[3].
In the third query, we can convert unit 6 into 1 unit of type 5 using the inverse of conversions[5], the inverse of conversions[2], conversions[1], then conversions[4].
In the fourth query, we can convert unit 4 into 2 units of type 6 using the inverse of conversions[3], the inverse of conversions[1], conversions[2], then conversions[5].
In the fifth query, we can convert unit 6 into 1/12 units of type 1 using the inverse of conversions[5], the inverse of conversions[2], then conversions[0]. We return 83333334 since it is the multiplicative inverse of 12.

Constraints

  • 2 <= n <= 10^5
  • conversions.length == n - 1
  • 0 <= sourceUniti, targetUniti < n
  • 1 <= conversionFactori <= 10^9
  • 1 <= q <= 10^5
  • queries.length == q
  • 0 <= unitAi, unitBi < n
  • It is guaranteed that unit 0 can be uniquely converted into any other unit through a combination of forward or backward conversions.

Solution

Method 1 – DFS/BFS for Conversion Ratios

Intuition

We can model the conversions as a bidirectional weighted graph. For each query, we can find the conversion ratio between two units by traversing the graph. To answer queries efficiently, we can precompute the conversion ratio from unit 0 to every other unit using DFS or BFS, then answer each query in O(1) using these ratios.

Approach

  1. Build a graph where each edge represents a conversion (and its inverse).
  2. Use DFS/BFS to compute the ratio from unit 0 to every other unit, storing as numerator/denominator (in reduced form).
  3. For each query, compute the ratio between unitAi and unitBi as (ratio[unitAi] / ratio[unitBi]).
  4. Return the result as p * q^-1 mod 1e9+7, where q^-1 is the modular inverse.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

#include <vector>
#include <numeric>
#define MOD 1000000007
using namespace std;

typedef long long ll;

ll modinv(ll a, ll m) {
    ll b = m, u = 1, v = 0;
    while (b) {
        ll t = a / b;
        a -= t * b; swap(a, b);
        u -= t * v; swap(u, v);
    }
    return (u % m + m) % m;
}

vector<int> unitConversionII(int n, vector<vector<int>>& conversions, vector<vector<int>>& queries) {
    vector<vector<pair<int, ll>>> g(n);
    for (auto& c : conversions) {
        int u = c[0], v = c[1], f = c[2];
        g[u].emplace_back(v, f);
        g[v].emplace_back(u, -f); // negative means inverse
    }
    vector<ll> num(n, 1), den(n, 1);
    vector<bool> vis(n);
    function<void(int)> dfs = [&](int u) {
        vis[u] = true;
        for (auto& [v, f] : g[u]) {
            if (!vis[v]) {
                if (f > 0) {
                    num[v] = num[u] * f;
                    den[v] = den[u];
                } else {
                    num[v] = num[u];
                    den[v] = den[u] * (-f);
                }
                ll g_ = gcd(num[v], den[v]);
                num[v] /= g_; den[v] /= g_;
                dfs(v);
            }
        }
    };
    dfs(0);
    vector<int> res;
    for (auto& q : queries) {
        int a = q[0], b = q[1];
        ll p = num[a] * den[b];
        ll qv = den[a] * num[b];
        ll g_ = gcd(p, qv);
        p /= g_; qv /= g_;
        ll ans = (p % MOD) * modinv(qv % MOD, MOD) % MOD;
        res.push_back(ans);
    }
    return res;
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

import java.util.*;
class Solution {
    static final int MOD = 1_000_000_007;
    public int[] unitConversionII(int n, int[][] conversions, int[][] queries) {
        List<List<long[]>> g = new ArrayList<>();
        for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
        for (int[] c : conversions) {
            g.get(c[0]).add(new long[]{c[1], c[2]});
            g.get(c[1]).add(new long[]{c[0], -c[2]});
        }
        long[] num = new long[n], den = new long[n];
        Arrays.fill(num, 1); Arrays.fill(den, 1);
        boolean[] vis = new boolean[n];
        dfs(0, g, num, den, vis);
        int[] res = new int[queries.length];
        for (int i = 0; i < queries.length; ++i) {
            int a = queries[i][0], b = queries[i][1];
            long p = num[a] * den[b];
            long qv = den[a] * num[b];
            long g_ = gcd(p, qv);
            p /= g_; qv /= g_;
            res[i] = (int)((p % MOD) * modinv(qv % MOD, MOD) % MOD);
        }
        return res;
    }
    void dfs(int u, List<List<long[]>> g, long[] num, long[] den, boolean[] vis) {
        vis[u] = true;
        for (long[] e : g.get(u)) {
            int v = (int)e[0]; long f = e[1];
            if (!vis[v]) {
                if (f > 0) {
                    num[v] = num[u] * f;
                    den[v] = den[u];
                } else {
                    num[v] = num[u];
                    den[v] = den[u] * -f;
                }
                long g_ = gcd(num[v], den[v]);
                num[v] /= g_; den[v] /= g_;
                dfs(v, g, num, den, vis);
            }
        }
    }
    long gcd(long a, long b) { return b == 0 ? a : gcd(b, a % b); }
    long modinv(long a, long m) {
        long b = m, u = 1, v = 0;
        while (b != 0) {
            long t = a / b;
            a -= t * b; long tmp = a; a = b; b = tmp;
            u -= t * v; tmp = u; u = v; v = tmp;
        }
        return (u % m + m) % m;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

from math import gcd
MOD = 10**9 + 7
def modinv(a, m):
    return pow(a, m-2, m)

def unitConversionII(n, conversions, queries):
    from collections import defaultdict, deque
    g = defaultdict(list)
    for u, v, f in conversions:
        g[u].append((v, f))
        g[v].append((u, -f))
    num = [1]*n
    den = [1]*n
    vis = [False]*n
    def dfs(u):
        vis[u] = True
        for v, f in g[u]:
            if not vis[v]:
                if f > 0:
                    num[v] = num[u] * f
                    den[v] = den[u]
                else:
                    num[v] = num[u]
                    den[v] = den[u] * (-f)
                g_ = gcd(num[v], den[v])
                num[v] //= g_
                den[v] //= g_
                dfs(v)
    dfs(0)
    res = []
    for a, b in queries:
        p = num[a] * den[b]
        qv = den[a] * num[b]
        g_ = gcd(p, qv)
        p //= g_
        qv //= g_
        ans = (p % MOD) * modinv(qv % MOD, MOD) % MOD
        res.append(ans)
    return res

Complexity

  • ⏰ Time complexity: O(n + q) — Build graph and DFS is O(n), each query is O(1).
  • 🧺 Space complexity: O(n) — For graph and ratios.