problemeasyalgorithmsleetcode-941leetcode 941leetcode941

Valid Mountain Array

EasyUpdated: Jul 31, 2025
Practice on:
LeetCode

Problem

Given an array of integers arr, return true if and only if it is a valid mountain array.

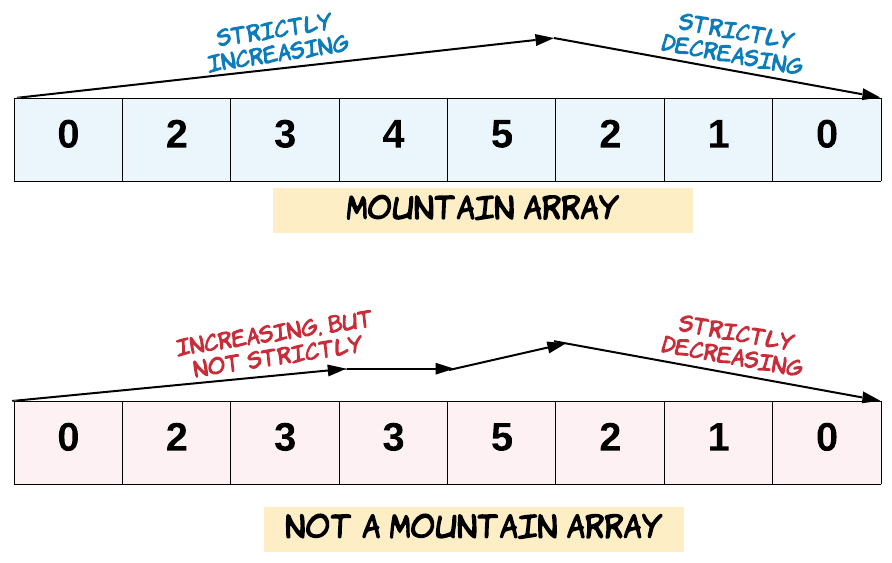
Recall that arr is a mountain array if and only if:

  • arr.length >= 3
  • There exists some i with 0 < i < arr.length - 1 such that:
  • arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
  • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

Examples

Example 1

Input: arr = [2,1]
Output: false

Example 2

Input: arr = [3,5,5]
Output: false

Example 3

Input: arr = [0,3,2,1]
Output: true

Constraints

  • 1 <= arr.length <= 10^4
  • 0 <= arr[i] <= 10^4

Solution

Method 1 – Single Pass (Two Pointers)

Intuition

We can walk up the mountain (increasing), then walk down (decreasing), and check if we used all elements and both up and down exist.

Approach

  1. Start from the beginning, walk up while arr[i] < arr[i+1].
  2. If we never went up or reached the end, return false.
  3. Walk down while arr[i] > arr[i+1].
  4. If we reach the end, it's a valid mountain.

Code

C++
#include <vector>
using namespace std;
bool validMountainArray(vector<int>& arr) {
    int n = arr.size(), i = 0;
    if (n < 3) return false;
    // walk up
    while (i + 1 < n && arr[i] < arr[i + 1]) i++;
    // peak can't be first or last
    if (i == 0 || i == n - 1) return false;
    // walk down
    while (i + 1 < n && arr[i] > arr[i + 1]) i++;
    return i == n - 1;
}
Go
func validMountainArray(arr []int) bool {
    n, i := len(arr), 0
    if n < 3 {
        return false
    }
    // walk up
    for i+1 < n && arr[i] < arr[i+1] {
        i++
    }
    // peak can't be first or last
    if i == 0 || i == n-1 {
        return false
    }
    // walk down
    for i+1 < n && arr[i] > arr[i+1] {
        i++
    }
    return i == n-1
}
Java
public boolean validMountainArray(int[] arr) {
    int n = arr.length, i = 0;
    if (n < 3) return false;
    // walk up
    while (i + 1 < n && arr[i] < arr[i + 1]) i++;
    // peak can't be first or last
    if (i == 0 || i == n - 1) return false;
    // walk down
    while (i + 1 < n && arr[i] > arr[i + 1]) i++;
    return i == n - 1;
}
Kotlin
fun validMountainArray(arr: IntArray): Boolean {
    val n = arr.size
    var i = 0
    if (n < 3) return false
    while (i + 1 < n && arr[i] < arr[i + 1]) i++
    if (i == 0 || i == n - 1) return false
    while (i + 1 < n && arr[i] > arr[i + 1]) i++
    return i == n - 1
}
Python
def validMountainArray(arr):
    n = len(arr)
    if n < 3:
        return False
    i = 0
    # walk up
    while i + 1 < n and arr[i] < arr[i + 1]:
        i += 1
    # peak can't be first or last
    if i == 0 or i == n - 1:
        return False
    # walk down
    while i + 1 < n and arr[i] > arr[i + 1]:
        i += 1
    return i == n - 1
Rust
pub fn valid_mountain_array(arr: Vec<i32>) -> bool {
    let n = arr.len();
    if n < 3 { return false; }
    let mut i = 0;
    while i + 1 < n && arr[i] < arr[i + 1] {
        i += 1;
    }
    if i == 0 || i == n - 1 { return false; }
    while i + 1 < n && arr[i] > arr[i + 1] {
        i += 1;
    }
    i == n - 1
}
TypeScript
function validMountainArray(arr: number[]): boolean {
    const n = arr.length;
    let i = 0;
    if (n < 3) return false;
    while (i + 1 < n && arr[i] < arr[i + 1]) i++;
    if (i === 0 || i === n - 1) return false;
    while (i + 1 < n && arr[i] > arr[i + 1]) i++;
    return i === n - 1;
}

Complexity

  • ⏰ Time complexity: O(n) — Single pass through the array.
  • 🧺 Space complexity: O(1) — Only a few variables are used.

Comments