Valid Parentheses

Problem

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.
3. Every close bracket has a corresponding open bracket of the same type.

Examples

Example 1

Input: s = "()"
Output: true

Example 2

Input: s = "()[]{}"
Output: true

can

Example 3

Input: s = "(]"
Output: false

More Examples

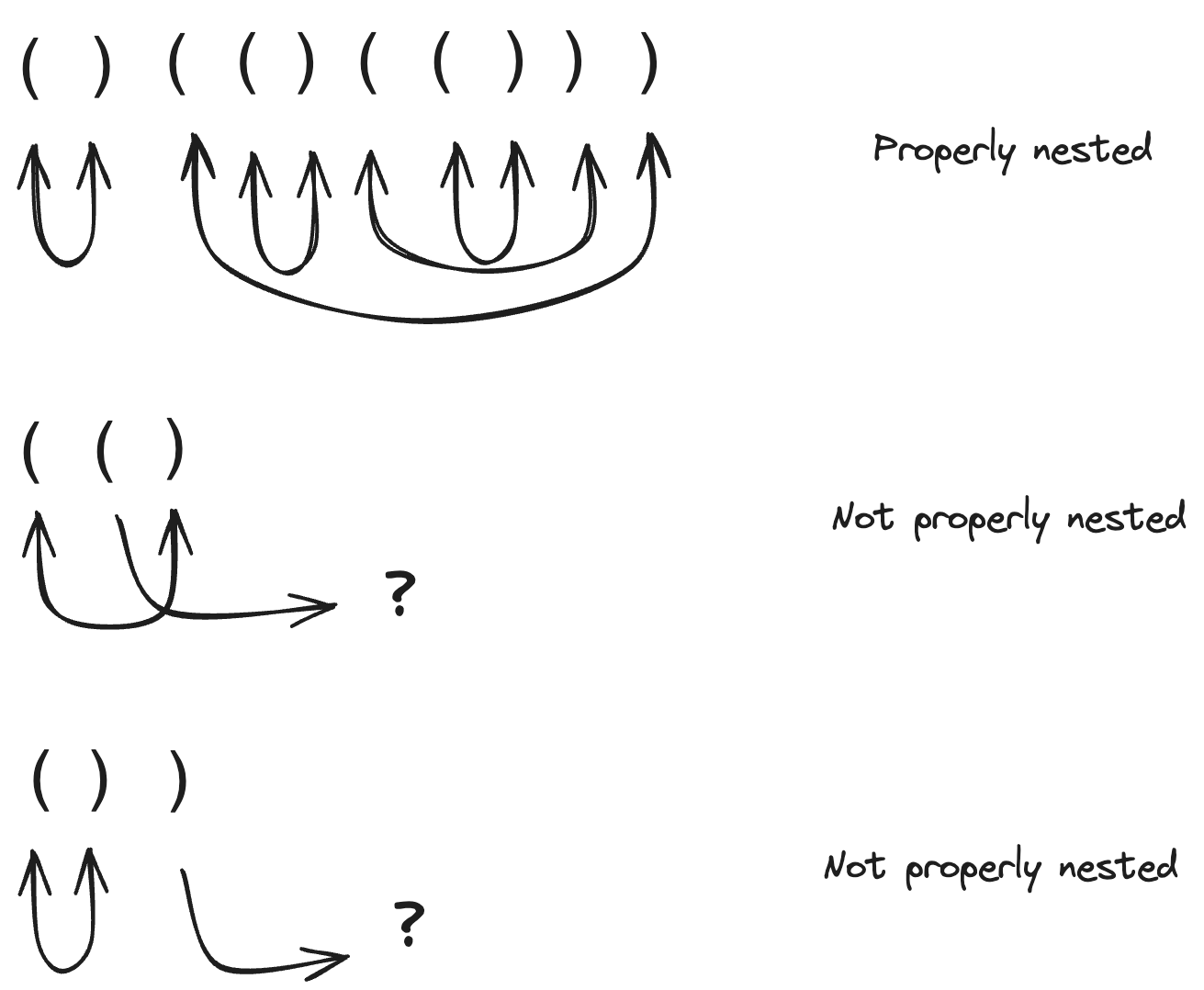
Follow up

• Only One Type of Parenthesis, Say ()

Solution

A typical problem which can be solved by using a stack data structure.

Version1 - When only 1 parenthesis type is present

Method 1 - Using stack and close to open map

Intuition

We observe a critical property: Last-In, First-Out (LIFO). The most recently opened bracket must be the first one closed. For example, in ([{}]), the { is opened last and must be closed by } before we can close [ or (. This strict ordering perfectly matches the behavior of a Stack data structure. When we encounter a closing bracket, it must match the bracket sitting at the top of our stack.

Approach

1. Initialize an empty stack and a map linking closing brackets to their corresponding opening brackets (e.g., ) -> ().
2. Iterate through the string character by character.
3. If we see an open bracket, push it onto the stack.
4. If we see a closing bracket:
   • Check if the stack is empty (invalid: no matching open).
   • Pop the top element and check if it matches the current closing bracket using the map (invalid: wrong type/order).
5. After the loop, return true if the stack is empty (all opened brackets were closed).

Video explanation

Here is the video explaining this method in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/6xIQh8tP0Eo" frameborder="0" allowfullscreen></iframe></div>

Complexity

• ⏰ Time complexity: O(n) – We iterate through each character in the string once.
• 🧺 Space complexity: O(n) – The stack can store up to all opening brackets in the worst case.

Code

C++

class Solution {
public:
    bool isValid(string s) {
        unordered_map<char, char> mapping = {{')', '('}, {'}', '{'}, {']', '['}};
        stack<char> stk;
        for (char ch : s) {
            if (mapping.find(ch) == mapping.end()) {
                stk.push(ch);
            } else {
                if (stk.empty() || stk.top() != mapping[ch]) {
                    return false;
                }
                stk.pop();
            }
        }
        return stk.empty();
    }
};

Go

func isValid(s string) bool {
    mapping := map[rune]rune{')': '(', '}': '{', ']': '['}
    stack := []rune{}
    for _, ch := range s {
        if _, ok := mapping[ch]; !ok {
            stack = append(stack, ch)
        } else {
            if len(stack) == 0 || stack[len(stack)-1] != mapping[ch] {
                return false
            }
            stack = stack[:len(stack)-1]
        }
    }
    return len(stack) == 0
}

Java

class Solution {
    public boolean isValid(String s) {
        // Map CLOSING brackets to their corresponding OPENING brackets
        Map<Character, Character> map = Map.of(')', '(', '}', '{', ']', '[');
        Stack<Character> stack = new Stack<>();

        for (char ch : s.toCharArray()) {
            // If it's NOT a closing bracket, it must be an opening bracket
            if (!map.containsKey(ch)) {
                stack.push(ch);
            } 
            // If it IS a closing bracket, we validate it
            else {
                if (stack.isEmpty() || stack.pop() != map.get(ch)) {
                    return false;
                }                
            }
        }
        return stack.isEmpty();
    }
}

Kotlin

class Solution {
    fun isValid(s: String): Boolean {
        val mapping = mapOf(')' to '(', '}' to '{', ']' to '[')
        val stack = ArrayDeque<Char>()
        for (ch in s) {
            if (!mapping.containsKey(ch)) {
                stack.addLast(ch)
            } else {
                if (stack.isEmpty() || stack.removeLast() != mapping[ch]) {
                    return false
                }
            }
        }
        return stack.isEmpty()
    }
}

Python

class Solution:
    def isValid(self, s: str) -> bool:
        # Map CLOSING brackets to their corresponding OPENING brackets
        mapping = {')': '(', '}': '{', ']': '['}
        stack = []

        for ch in s:
            # If it's NOT a closing bracket, it's an opening bracket
            if ch not in mapping:
                stack.append(ch)
            # If it IS a closing bracket, validate against the stack
            else:
                if not stack or stack.pop() != mapping[ch]:
                    return False                
                
        return not stack

Rust

impl Solution {
    pub fn is_valid(s: String) -> bool {
        let mapping = [(')', '('), ('}', '{'), (']', '[')].iter().cloned().collect::<std::collections::HashMap<char, char>>();
        let mut stack = Vec::new();
        for ch in s.chars() {
            if !mapping.contains_key(&ch) {
                stack.push(ch);
            } else {
                if stack.is_empty() || stack.pop().unwrap() != mapping[&ch] {
                    return false;
                }
            }
        }
        stack.is_empty()
    }
}

Method 2 - Using Stack and open to close map

Why Stack?

Since the last bracket that is opened must also be the first one to be closed, it makes sense to use a data structure that uses the Last In, First Out (LIFO) principle. Therefore, a stack is a good choice here.

Code

C++

class Solution {
public:
    bool isValid(string s) {
        unordered_map<char, char> parenthese = {{'(', ')'}, {'{', '}'}, {'[', ']'}};
        stack<char> stk;
        for (char c : s) {
            if (parenthese.count(c)) {
                stk.push(c);
            } else {
                if (stk.empty()) return false;
                char cKey = stk.top(); stk.pop();
                char cVal = parenthese[cKey];
                if (cVal != c) return false;
            }
        }
        return stk.empty();
    }
};

Go

type Solution struct{}

func (Solution) isValid(s string) bool {
    parenthese := map[rune]rune{'(': ')', '{': '}', '[': ']'}
    stack := []rune{}
    for _, c := range s {
        if _, ok := parenthese[c]; ok {
            stack = append(stack, c)
        } else {
            if len(stack) == 0 {
                return false
            }
            cKey := stack[len(stack)-1]
            stack = stack[:len(stack)-1]
            cVal := parenthese[cKey]
            if cVal != c {
                return false
            }
        }
    }
    return len(stack) == 0
}

Java

class Solution {
    public boolean isValid(String s) {
        Map<Character, Character> parenthese = new HashMap<>();
        parenthese.put('(', ')');
        parenthese.put('{', '}');
        parenthese.put('[', ']');
        Stack<Character> stack = new Stack<>();
        for (char c : s.toCharArray()) {
            if (parenthese.containsKey(c)) {
                stack.push(c);
            } else {
                if (stack.isEmpty()) {
                    return false;
                }
                char cKey = stack.pop();
                char cVal = parenthese.get(cKey);
                if (cVal != c) {
                    return false;
                }
            }
        }
        return stack.isEmpty();
    }
}

Kotlin

class Solution {
    fun isValid(s: String): Boolean {
        val parenthese = mapOf('(' to ')', '{' to '}', '[' to ']')
        val stack = ArrayDeque<Char>()
        for (c in s) {
            if (parenthese.containsKey(c)) {
                stack.addLast(c)
            } else {
                if (stack.isEmpty()) return false
                val cKey = stack.removeLast()
                val cVal = parenthese[cKey]
                if (cVal != c) return false
            }
        }
        return stack.isEmpty()
    }
}

Python

class Solution:
    def isValid(self, s: str) -> bool:
        parenthese = {'(': ')', '{': '}', '[': ']'}
        stack = []
        for c in s:
            if c in parenthese:
                stack.append(c)
            else:
                if not stack:
                    return False
                cKey = stack.pop()
                cVal = parenthese[cKey]
                if cVal != c:
                    return False
        return not stack

Rust

impl Solution {
    pub fn is_valid(s: String) -> bool {
        let parenthese = [('(', ')'), ('{', '}'), ('[', ']')].iter().cloned().collect::<std::collections::HashMap<char, char>>();
        let mut stack = Vec::new();
        for c in s.chars() {
            if parenthese.contains_key(&c) {
                stack.push(c);
            } else {
                if stack.is_empty() {
                    return false;
                }
                let c_key = stack.pop().unwrap();
                let c_val = parenthese[&c_key];
                if c_val != c {
                    return false;
                }
            }
        }
        stack.is_empty()
    }
}

Typescript

class Solution {
    isValid(s: string): boolean {
        const parenthese: {[key: string]: string} = {'(': ')', '{': '}', '[': ']'};
        const stack: string[] = [];
        for (const c of s) {
            if (c in parenthese) {
                stack.push(c);
            } else {
                if (stack.length === 0) return false;
                const cKey = stack.pop()!;
                const cVal = parenthese[cKey];
                if (cVal !== c) return false;
            }
        }
        return stack.length === 0;
    }
}

Complexity

• ⏰ Time complexity: O(n) – We process each character in the string exactly once.
• 🧺 Space complexity: O(n) – The stack can grow up to the length of the string in the worst case.

Dry Run

Lets see algo in action.

Example 1

Consider the following expression {([])}

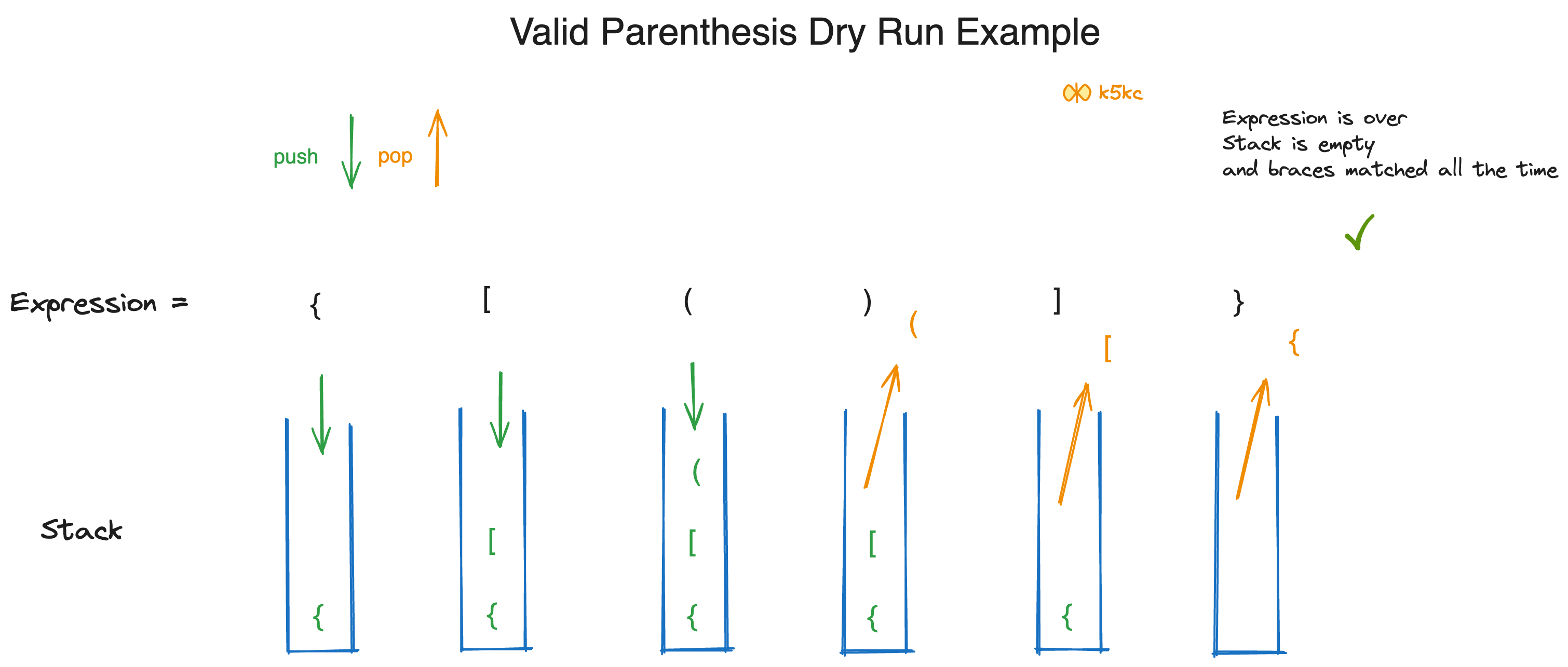
Example 2

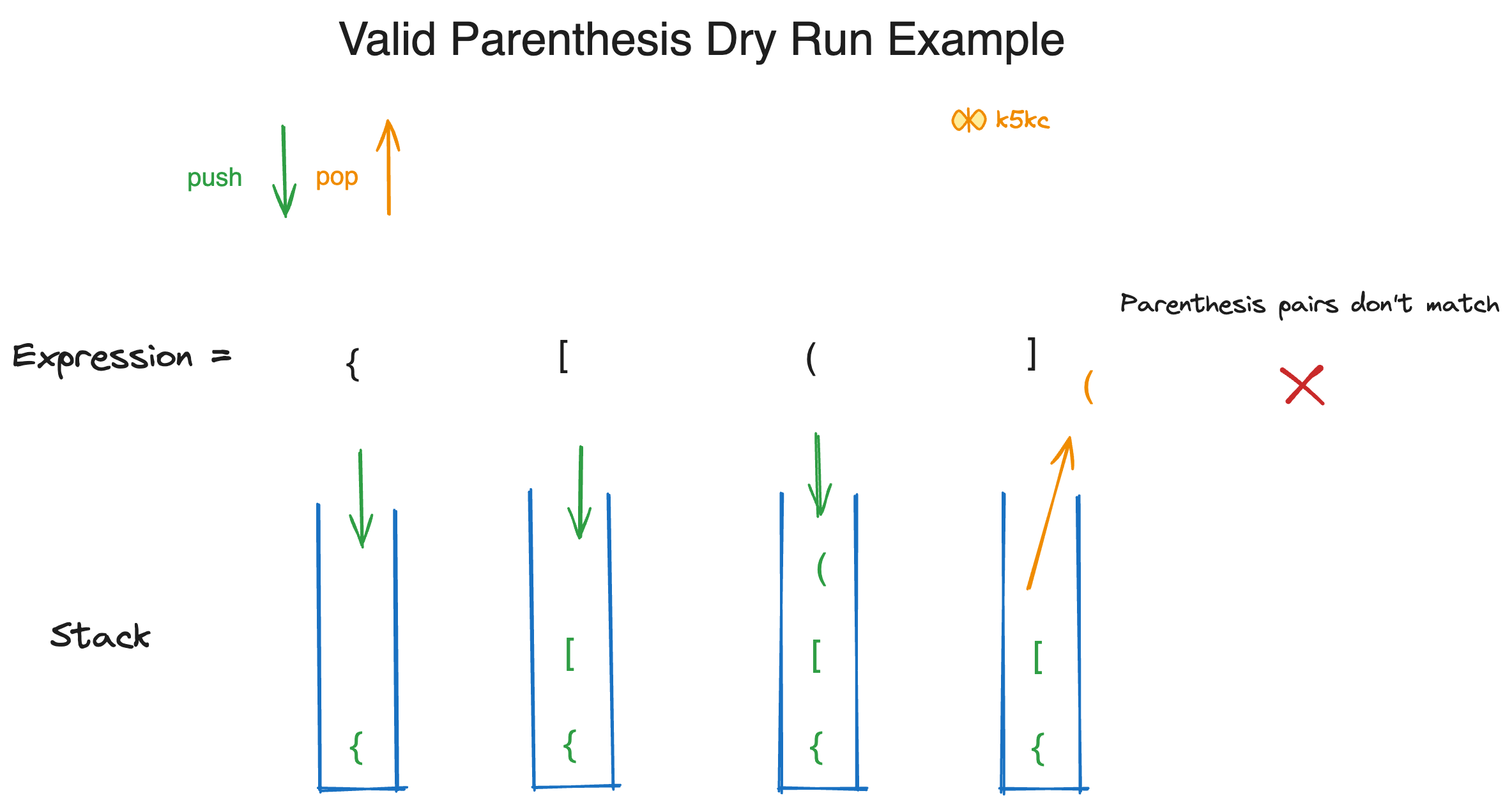
Example 3

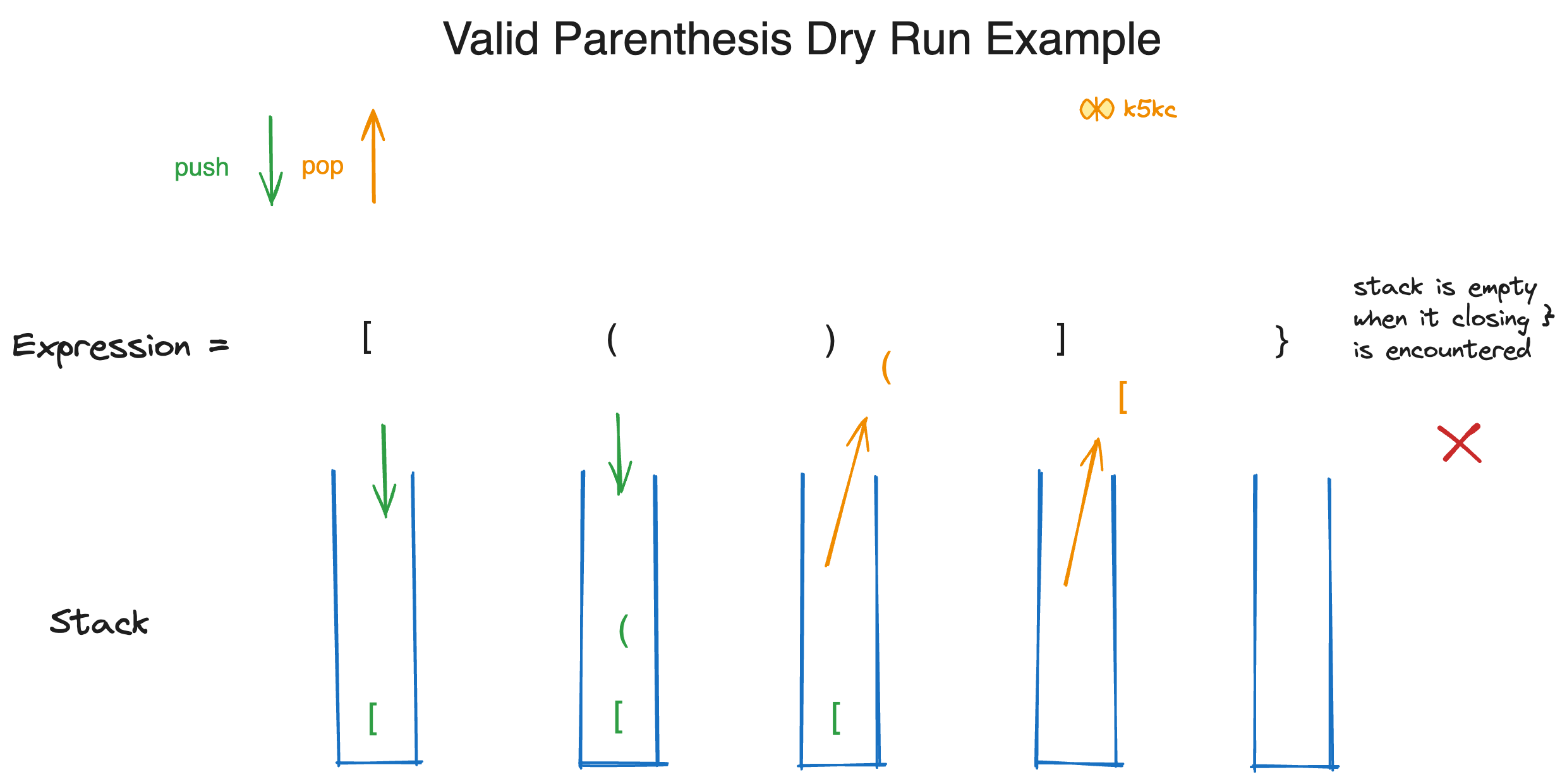
Example 4

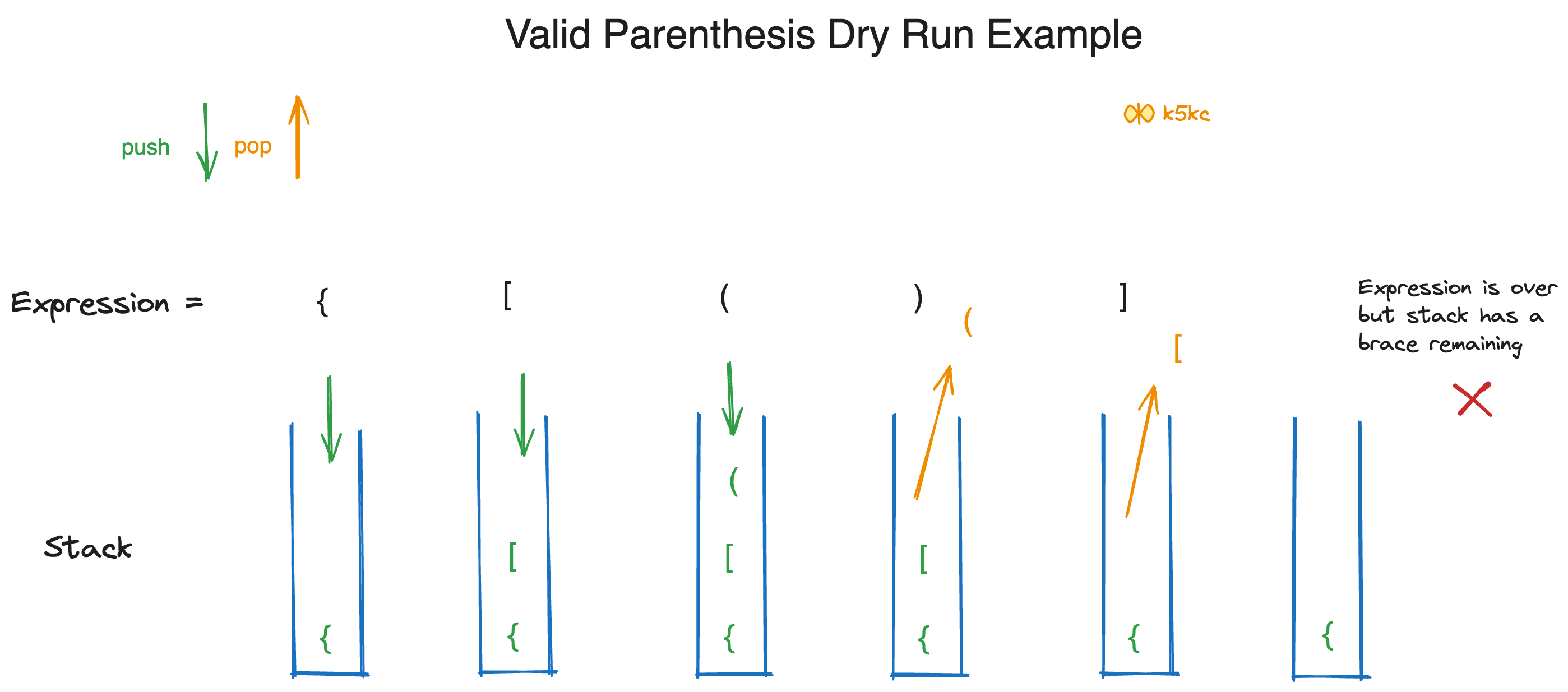
Follow up - When there is only one type of parentheses

Method 1 - Using Counter

Intuition

The key insight is that for a string with only one type of parenthesis, we do not need a stack. We can simply count the number of open and close parentheses as we scan the string. If at any point the number of closing parentheses exceeds the number of opening ones, the string is invalid. At the end, the count must be zero for the string to be valid.

Approach

1. Initialize a counter to zero.
2. Iterate through each character in the string.
3. Increment the counter for every '('. Decrement for every ')'.
4. If the counter ever becomes negative, return false immediately (more closing than opening).
5. After the loop, return true if the counter is zero (all parentheses matched), otherwise false.

Pseudocode

Boolean: IsProperlyNested(String: expression)
	Integer: counter = 0
	For Each ch In expression
		If (ch == '(') Then counter = counter + 1
			Else If (ch == ')') Then
				counter = counter - 1
			If (counter < 0) Then Return False
		End If
	Next ch
	If (counter == 0) Then Return True
	 Else Return False
IsProperlyNested

Complexity

• ⏰ Time complexity: O(n) – We scan the string once, incrementing or decrementing the counter.
• 🧺 Space complexity: O(1) – Only a single integer counter is used regardless of input size.

Code

C++

class Solution {
public:
    bool isProperlyNested(const string& expression) {
        int counter = 0;
        for (char ch : expression) {
            if (ch == '(') counter++;
            else if (ch == ')') {
                counter--;
                if (counter < 0) return false;
            }
        }
        return counter == 0;
    }
};

Go

type Solution struct{}

func (Solution) isProperlyNested(expression string) bool {
    counter := 0
    for _, ch := range expression {
        if ch == '(' {
            counter++
        } else if ch == ')' {
            counter--
            if counter < 0 {
                return false
            }
        }
    }
    return counter == 0
}

Java

class Solution {
    public boolean isProperlyNested(String expression) {
        int counter = 0;
        for (char ch : expression.toCharArray()) {
            if (ch == '(') counter++;
            else if (ch == ')') {
                counter--;
                if (counter < 0) return false;
            }
        }
        return counter == 0;
    }
}

Kotlin

class Solution {
    fun isProperlyNested(expression: String): Boolean {
        var counter = 0
        for (ch in expression) {
            if (ch == '(') counter++
            else if (ch == ')') {
                counter--
                if (counter < 0) return false
            }
        }
        return counter == 0
    }
}

Python

class Solution:
    def isProperlyNested(self, expression: str) -> bool:
        counter = 0
        for ch in expression:
            if ch == '(': counter += 1
            elif ch == ')':
                counter -= 1
                if counter < 0:
                    return False
        return counter == 0

Rust

impl Solution {
    pub fn is_properly_nested(expression: &str) -> bool {
        let mut counter = 0;
        for ch in expression.chars() {
            if ch == '(' {
                counter += 1;
            } else if ch == ')' {
                counter -= 1;
                if counter < 0 {
                    return false;
                }
            }
        }
        counter == 0
    }
}

Typescript

class Solution {
    isProperlyNested(expression: string): boolean {
        let counter = 0;
        for (const ch of expression) {
            if (ch === '(') counter++;
            else if (ch === ')') {
                counter--;
                if (counter < 0) return false;
            }
        }
        return counter === 0;
    }
}