Verify Preorder Serialization of a Binary Tree

Problem

One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node's value. If it is a null node, we record using a sentinel value such as '#'.

      9
    /   \
   3     2
  / \   / \
 4   1 #   6
/ \ / \   / \
# # # #  #   #

For example, the above binary tree can be serialized to the string "9,3,4,#,#,1,#,#,2,#,6,#,#", where '#' represents a null node.

Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.

It is guaranteed that each comma-separated value in the string must be either an integer or a character '#' representing null pointer.

You may assume that the input format is always valid.

• For example, it could never contain two consecutive commas, such as "1,,3".

Note: You are not allowed to reconstruct the tree.

Examples

Example 1:

Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
Output:
 true

Example 2:

Input: preorder = "1,#"
Output:
 false

Example 3:

Input: preorder = "9,#,#,1"
Output:
 false

Solution

Method 1 - Using Stack

We can keep trimming the leaves until there are no more to remove. For example, if a sequence like 4 # # is encountered, we simplify it to # and continue. A stack is a suitable data structure for this purpose.

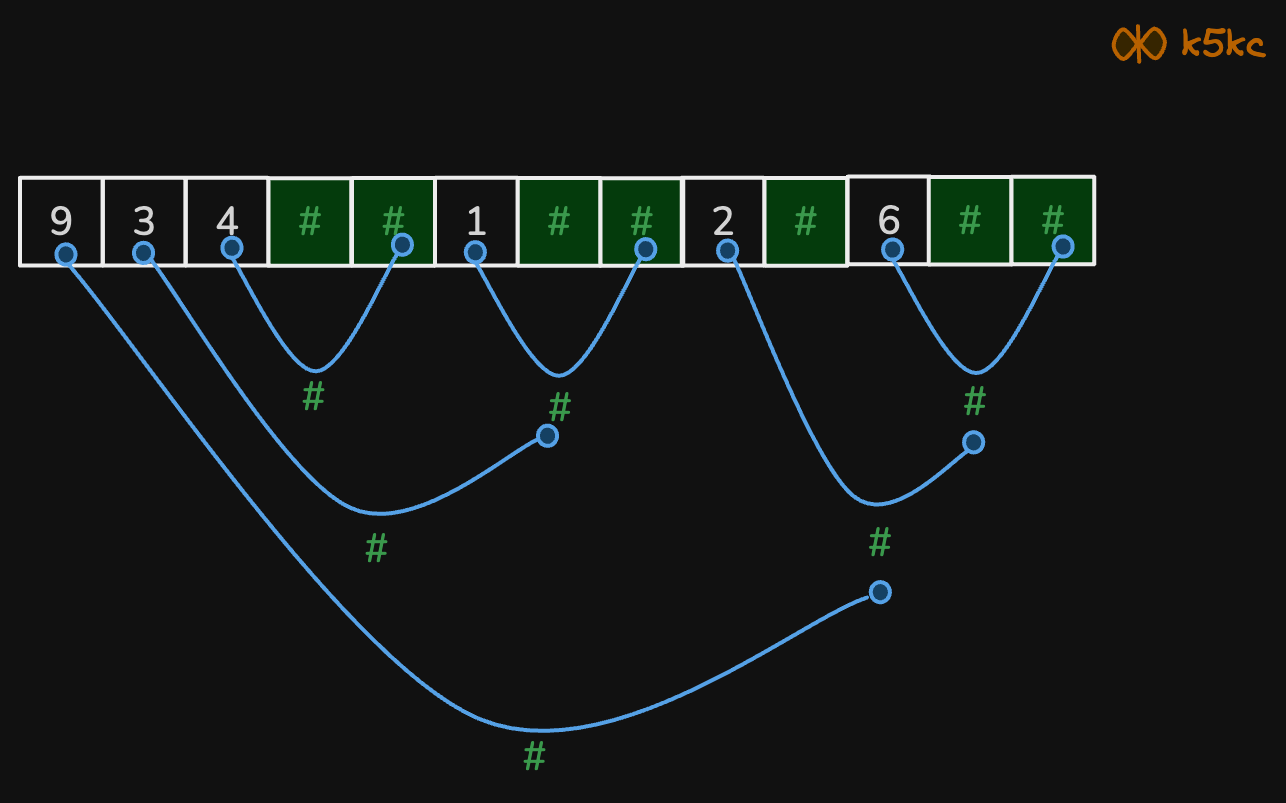
When iterating through the preorder traversal string, for each node:

• Case 1: You encounter a number c (non-null node):
  • A number represents the root of a new subtree. You consume one slot and push 2 slots onto the stack, as this node will have two children.
• Case 2: You encounter a # (null node):
  • Subcase 2.1: The top of the stack represents a positive count (remaining slots):
    • This null node consumes 1 slot, decrementing the top of the stack by 1.
    • If the slot count at the top becomes 0, pop the stack as no further nodes can be added to this subtree.
  • Subcase 2.2: The top of the stack already represents a completed subtree (slot 0):
    • This signifies that the null node belongs to a previously completed right child.
    • Continue popping the stack until it either becomes empty or the top of the stack indicates remaining slots for further children.

After processing all nodes

• If the stack is empty, the serialization is valid.
• If the stack is non-empty, the serialization is invalid, indicating there were unconsumed slots.

Code

Java

class Solution {
    public boolean isValidSerialization(String preorder) {
        String[] nodes = preorder.split(",");
        Stack<Integer> stack = new Stack<>();
        // Start with one slot for the root
        stack.push(1);
        
        for (String node : nodes) {
            // If no slots are available, return false
            if (stack.isEmpty()) {
                return false;
            }
            
            // Consume one slot for the current node
            stack.push(stack.pop() - 1);
            
            // Remove slot if the count reaches zero
            if (stack.peek() == 0) {
                stack.pop();
            }
            
            // Non-null nodes create two additional slots
            if (!node.equals("#")) {
                stack.push(2);
            }
        }
        
        // At the end, the stack should be empty (all slots filled properly)
        return stack.isEmpty();
    }
}

Python

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        nodes: List[str] = preorder.split(",")
        stack: List[int] = [1]  # Start with one slot for the root
        
        for node in nodes:
            # If no slots are available, return False
            if not stack:
                return False
            
            # Consume one slot for the current node
            stack[-1] -= 1
            
            # Remove slot if the count reaches zero
            if stack[-1] == 0:
                stack.pop()
            
            # Non-null nodes create two additional slots
            if node != "#":
                stack.append(2)
        
        # At the end, stack should be empty (all slots filled properly)
        return not stack

Complexity

• ⏰ Time complexity: O(n): Traversal of the preorder string (split by commas).
• 🧺 Space complexity: O(n): Maximum size of the stack is the number of nodes.

Dry Running the Code:

preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
curr=9
stk=[9]

curr=3
stk=[9,3]

curr=4
stk=[9,3,4]

curr=#
stk=[9,3,4,#]

curr=#
stk=[9,3,#]
explanation: We cancelled the whole subtree with root as 4 and replaced it with #

curr=1
stk=[9,3,#,1]

curr=#
stk=[9,3,#,1,#]

curr=#
stk=[9,3,#,1,#] => [9,3,#] => [9] =>  [9,#]
explanation: We cancelled root 1, but top of the stack was still #, so we popped out another 2 values and replaced it with #
Lets see what we did here. We just replaced the entire left subtree with #:

      9                          9 
    /   \                      /   \
   3     2                    #     2
  / \   / \            =>          / \
 4   1 #   6                      #   6
/ \ / \   / \                        / \
# # # #  #   #                      #   #


curr=2
stk=[9,#,2]

curr=#
stk=[9,#,2,#]

curr=6
stk=[9,#,2,#,6]

curr=#
stk=[9,#,2,#,6,#]

curr=#
stk=[9,#,2,#,6,#] => [9,#,2,#,6,#] => [9,#,2,#] => [9,#] => [#]

So, we processed the tree and replace it with #.

Method 2 - Using a List Like a Stack

Code

Java

class Solution {
	public boolean isValidSerialization(String preorder) {
		List<String> list = new LinkedList<String> ();
		String[] arr = preorder.split(",");
	
		for (int i = 0; i<arr.length; i++) {
			list.add(arr[i]);
	
			while (list.size() >= 3 &&
				list.get(list.size() - 1).equals("#") &&
				list.get(list.size() - 2).equals("#") &&
				!list.get(list.size() - 3).equals("#")) {
	
				list.remove(list.size() - 1);
				list.remove(list.size() - 1);
				list.remove(list.size() - 1);
	
				list.add("#");
			}
	
		}
	
		if (list.size() == 1 && list.get(0).equals("#"))
			return true;
		else
			return false;
	}
}

Method 3 - Using in-degree and out-degree on tree nodes

In a binary tree, we can describe each node as contributing to the indegree and outdegree:

• Non-null nodes (integer):
  • Provide 2 outdegrees (for their left and right children).
  • Contribute 1 indegree by occupying one position in the tree (as a child of their parent).
  • Except the root, which has no parent and therefore does not contribute an indegree.
• Null nodes ('#'):
  • Provide 0 outdegrees (null nodes cannot have children).
  • Contribute 1 indegree by occupying one position in the tree.

To validate whether the given preorder serialization is correct:

1. Use a variable diff to track the difference between total outdegree and total indegree:
   • Start with diff = 1 (the root provides an outdegree for the tree but does not consume an indegree).
2. Iterate through the nodes:
   • Decrease diff by 1 for each node (all nodes consume one indegree).
   • If the node is non-null, increase diff by 2 to account for its outdegrees.
3. If at any point diff < 0, the serialization is invalid (indegree exceeds outdegree, indicating an imbalance).
4. At the end, check if diff == 0. A valid serialization will have balanced indegree and outdegree.

Code

Java

class Solution {
    public boolean isValidSerialization(String preorder) {
        String[] nodes = preorder.split(",");
        int diff = 1; // Start with outdegree for the root node

        for (String node : nodes) {
            // Consume one indegree for the current node
            diff--;

            // If diff becomes negative, the serialization is invalid
            if (diff < 0) {
                return false;
            }

            // Non-null node contributes 2 outdegrees
            if (!node.equals("#")) {
                diff += 2;
            }
        }

        // Serialization is valid if all indegree and outdegree are balanced
        return diff == 0;
    }
}

Python

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        nodes = preorder.split(",")
        diff: int = 1  # Start with outdegree for the root node

        for node in nodes:
            # Consume one indegree for the current node
            diff -= 1

            # If diff becomes negative, the serialization is invalid
            if diff < 0:
                return False

            # Non-null node contributes 2 outdegrees
            if node != "#":
                diff += 2

        # Serialization is valid if all indegree and outdegree are balanced
        return diff == 0

Complexity

• ⏰ Time complexity: O(n)
  • The traversal of all nodes in the preorder string takes linear time.
  • Splitting the string using split(",") also takes linear time.
• 🧺 Space complexity: O(n)
  • We require space for the nodes array after splitting the string.