Walking Robot Simulation II
Problem
A width x height grid is on an XY-plane with the bottom-left cell at
(0, 0) and the top-right cell at (width - 1, height - 1). The grid is aligned with the four cardinal directions ("North", "East", "South", and
"West"). A robot is initially at cell (0, 0) facing direction
"East".
The robot can be instructed to move for a specific number of steps. For each step, it does the following.
- Attempts to move forward one cell in the direction it is facing.
- If the cell the robot is moving to is out of bounds , the robot instead turns 90 degrees counterclockwise and retries the step.
After the robot finishes moving the number of steps required, it stops and awaits the next instruction.
Implement the Robot class:
Robot(int width, int height)Initializes thewidth x heightgrid with the robot at(0, 0)facing"East".void step(int num)Instructs the robot to move forwardnumsteps.int[] getPos()Returns the current cell the robot is at, as an array of length 2,[x, y].String getDir()Returns the current direction of the robot,"North","East","South", or"West".
Examples
Example 1
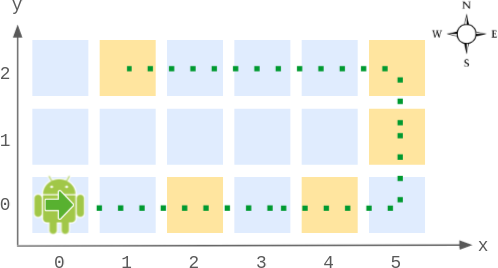
**Input**
["Robot", "step", "step", "getPos", "getDir", "step", "step", "step", "getPos", "getDir"]
[[6, 3], [2], [2], [], [], [2], [1], [4], [], []]
**Output**
[null, null, null, [4, 0], "East", null, null, null, [1, 2], "West"]
**Explanation**
Robot robot = new Robot(6, 3); // Initialize the grid and the robot at (0, 0) facing East.
robot.step(2); // It moves two steps East to (2, 0), and faces East.
robot.step(2); // It moves two steps East to (4, 0), and faces East.
robot.getPos(); // return [4, 0]
robot.getDir(); // return "East"
robot.step(2); // It moves one step East to (5, 0), and faces East.
// Moving the next step East would be out of bounds, so it turns and faces North.
// Then, it moves one step North to (5, 1), and faces North.
robot.step(1); // It moves one step North to (5, 2), and faces **North** (not West).
robot.step(4); // Moving the next step North would be out of bounds, so it turns and faces West.
// Then, it moves four steps West to (1, 2), and faces West.
robot.getPos(); // return [1, 2]
robot.getDir(); // return "West"
Constraints
2 <= width, height <= 1001 <= num <= 10^5- At most
104calls in total will be made tostep,getPos, andgetDir.
Solution
Method 1 – Perimeter Simulation with Modulo
Intuition
The robot always moves along the grid's perimeter in a fixed order. We can precompute the perimeter path and use modulo arithmetic to efficiently simulate large numbers of steps.
Approach
Store the perimeter path as a list of (x, y, dir) states. For each step, move along this path, wrapping around with modulo. This allows O(1) step and query operations.
Code
C++
#include <vector>
#include <string>
using namespace std;
class Robot {
vector<pair<int,int>> path;
vector<string> dirs;
int n, idx;
public:
Robot(int width, int height) {
for (int x = 0; x < width; ++x) {
path.emplace_back(x, 0); dirs.push_back("East");
}
for (int y = 1; y < height; ++y) {
path.emplace_back(width-1, y); dirs.push_back("North");
}
for (int x = width-2; x >= 0; --x) {
path.emplace_back(x, height-1); dirs.push_back("West");
}
for (int y = height-2; y > 0; --y) {
path.emplace_back(0, y); dirs.push_back("South");
}
n = path.size(); idx = 0;
}
void step(int num) { idx = (idx + num) % n; }
vector<int> getPos() { return {path[idx].first, path[idx].second}; }
string getDir() { return dirs[idx]; }
};
Go
type Robot struct {
path [][3]interface{}
n, idx int
}
func Constructor(width int, height int) Robot {
path := make([][3]interface{}, 0)
for x := 0; x < width; x++ {
path = append(path, [3]interface{}{x, 0, "East"})
}
for y := 1; y < height; y++ {
path = append(path, [3]interface{}{width-1, y, "North"})
}
for x := width-2; x >= 0; x-- {
path = append(path, [3]interface{}{x, height-1, "West"})
}
for y := height-2; y > 0; y-- {
path = append(path, [3]interface{}{0, y, "South"})
}
return Robot{path, len(path), 0}
}
func (r *Robot) Step(num int) {
r.idx = (r.idx + num) % r.n
}
func (r *Robot) GetPos() []int {
return []int{r.path[r.idx][0].(int), r.path[r.idx][1].(int)}
}
func (r *Robot) GetDir() string {
return r.path[r.idx][2].(string)
}
Java
import java.util.*;
class Robot {
private int[][] path;
private String[] dirs;
private int n, idx;
public Robot(int width, int height) {
List<int[]> p = new ArrayList<>();
List<String> d = new ArrayList<>();
for (int x = 0; x < width; x++) {
p.add(new int[]{x, 0}); d.add("East");
}
for (int y = 1; y < height; y++) {
p.add(new int[]{width-1, y}); d.add("North");
}
for (int x = width-2; x >= 0; x--) {
p.add(new int[]{x, height-1}); d.add("West");
}
for (int y = height-2; y > 0; y--) {
p.add(new int[]{0, y}); d.add("South");
}
n = p.size();
path = p.toArray(new int[n][2]);
dirs = d.toArray(new String[n]);
idx = 0;
}
public void step(int num) {
idx = (idx + num) % n;
}
public int[] getPos() {
return path[idx];
}
public String getDir() {
return dirs[idx];
}
}
Kotlin
class Robot(width: Int, height: Int) {
private val path = mutableListOf<Triple<Int, Int, String>>()
private var idx = 0
private val n: Int
init {
for (x in 0 until width) path.add(Triple(x, 0, "East"))
for (y in 1 until height) path.add(Triple(width-1, y, "North"))
for (x in width-2 downTo 0) path.add(Triple(x, height-1, "West"))
for (y in height-2 downTo 1) path.add(Triple(0, y, "South"))
n = path.size
}
fun step(num: Int) { idx = (idx + num) % n }
fun getPos(): IntArray { val (x, y, _) = path[idx]; return intArrayOf(x, y) }
fun getDir(): String { return path[idx].third }
}
Python
from typing import List
class Robot:
def __init__(self, width: int, height: int):
self.width = width
self.height = height
self.path = []
# Build the perimeter path and directions
# East (0,0) to (width-1,0)
for x in range(width):
self.path.append((x, 0, 'East'))
# North (width-1,1) to (width-1,height-1)
for y in range(1, height):
self.path.append((width-1, y, 'North'))
# West (width-2,height-1) to (0,height-1)
for x in range(width-2, -1, -1):
self.path.append((x, height-1, 'West'))
# South (0,height-2) to (0,1)
for y in range(height-2, 0, -1):
self.path.append((0, y, 'South'))
self.n = len(self.path)
self.idx = 0 # current index in path
def step(self, num: int) -> None:
self.idx = (self.idx + num) % self.n
def getPos(self) -> List[int]:
x, y, _ = self.path[self.idx]
return [x, y]
def getDir(self) -> str:
_, _, d = self.path[self.idx]
return d
Rust
pub struct Robot {
path: Vec<(i32, i32, &'static str)>,
idx: usize,
n: usize,
}
impl Robot {
pub fn new(width: i32, height: i32) -> Self {
let mut path = Vec::new();
for x in 0..width { path.push((x, 0, "East")); }
for y in 1..height { path.push((width-1, y, "North")); }
for x in (0..width-1).rev() { path.push((x, height-1, "West")); }
for y in (1..height-1).rev() { path.push((0, y, "South")); }
let n = path.len();
Self { path, idx: 0, n }
}
pub fn step(&mut self, num: i32) { self.idx = ((self.idx as i32 + num) % self.n as i32) as usize; }
pub fn get_pos(&self) -> Vec<i32> { let (x, y, _) = self.path[self.idx]; vec![x, y] }
pub fn get_dir(&self) -> &str { let (_, _, d) = self.path[self.idx]; d }
}
TypeScript
class Robot {
private path: [number, number, string][] = [];
private idx = 0;
private n: number;
constructor(width: number, height: number) {
for (let x = 0; x < width; x++) this.path.push([x, 0, 'East']);
for (let y = 1; y < height; y++) this.path.push([width-1, y, 'North']);
for (let x = width-2; x >= 0; x--) this.path.push([x, height-1, 'West']);
for (let y = height-2; y > 0; y--) this.path.push([0, y, 'South']);
this.n = this.path.length;
}
step(num: number) { this.idx = (this.idx + num) % this.n; }
getPos(): number[] { const [x, y] = this.path[this.idx]; return [x, y]; }
getDir(): string { return this.path[this.idx][2]; }
}
Complexity
- ⏰ Time complexity:
O(1)per operation after initialization (which isO(width+height)). - 🧺 Space complexity:
O(width+height)for the perimeter path.