problemeasyalgorithmsleetcode-1637leetcode 1637leetcode1637

Widest Vertical Area Between Two Points Containing No Points

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

Given n points on a 2D plane where points[i] = [xi, yi], Return _ the widest vertical area between two points such that no points are inside the area._

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

Examples

Example 1


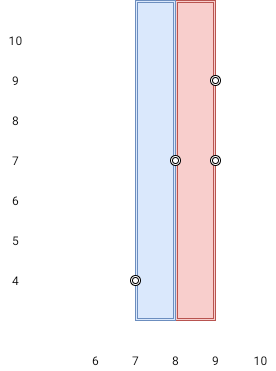
![](https://assets.leetcode.com/uploads/2020/09/19/points3.png)​

Input: points = [[8,7],[9,9],[7,4],[9,7]]
Output: 1
Explanation: Both the red and the blue area are optimal.

Example 2

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
Output: 3

Constraints

  • n == points.length
  • 2 <= n <= 10^5
  • points[i].length == 2
  • 0 <= xi, yi <= 10^9

Solution

Method 1 – Sort and Find Maximum Gap

Intuition

The widest vertical area is the largest gap between any two x-coordinates after sorting. The y-coordinates are irrelevant.

Approach

  1. Extract all x-coordinates from the points.
  2. Sort the x-coordinates.
  3. Find the maximum difference between consecutive x-coordinates.
  4. Return the maximum gap found.

Code

C++
class Solution {
public:
    int maxWidthOfVerticalArea(vector<vector<int>>& points) {
        vector<int> xs;
        for (auto& p : points) xs.push_back(p[0]);
        sort(xs.begin(), xs.end());
        int ans = 0;
        for (int i = 1; i < xs.size(); ++i) {
            ans = max(ans, xs[i] - xs[i-1]);
        }
        return ans;
    }
};
Go
import "sort"
func maxWidthOfVerticalArea(points [][]int) int {
    xs := make([]int, len(points))
    for i, p := range points {
        xs[i] = p[0]
    }
    sort.Ints(xs)
    ans := 0
    for i := 1; i < len(xs); i++ {
        if xs[i]-xs[i-1] > ans {
            ans = xs[i] - xs[i-1]
        }
    }
    return ans
}
Java
import java.util.*;
class Solution {
    public int maxWidthOfVerticalArea(int[][] points) {
        int n = points.length;
        int[] xs = new int[n];
        for (int i = 0; i < n; i++) xs[i] = points[i][0];
        Arrays.sort(xs);
        int ans = 0;
        for (int i = 1; i < n; i++) ans = Math.max(ans, xs[i] - xs[i-1]);
        return ans;
    }
}
Kotlin
class Solution {
    fun maxWidthOfVerticalArea(points: Array<IntArray>): Int {
        val xs = points.map { it[0] }.sorted()
        return xs.zipWithNext { a, b -> b - a }.maxOrNull() ?: 0
    }
}
Python
from typing import List
class Solution:
    def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:
        xs = sorted(p[0] for p in points)
        return max(xs[i] - xs[i-1] for i in range(1, len(xs)))
Rust
impl Solution {
    pub fn max_width_of_vertical_area(points: Vec<Vec<i32>>) -> i32 {
        let mut xs: Vec<i32> = points.iter().map(|p| p[0]).collect();
        xs.sort();
        xs.windows(2).map(|w| w[1] - w[0]).max().unwrap_or(0)
    }
}
TypeScript
class Solution {
    maxWidthOfVerticalArea(points: number[][]): number {
        const xs = points.map(p => p[0]).sort((a, b) => a - b);
        let ans = 0;
        for (let i = 1; i < xs.length; i++) {
            ans = Math.max(ans, xs[i] - xs[i-1]);
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n log n) — Sorting the x-coordinates dominates, where n is the number of points.
  • 🧺 Space complexity: O(n) — For storing the x-coordinates.

Comments