Word Break 2 - Construct a sentence

Problem

Given a string s and a dictionary of strings wordDict, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences in any order.

Note that the same word in the dictionary may be reused multiple times in the segmentation.

Examples

Example 1:

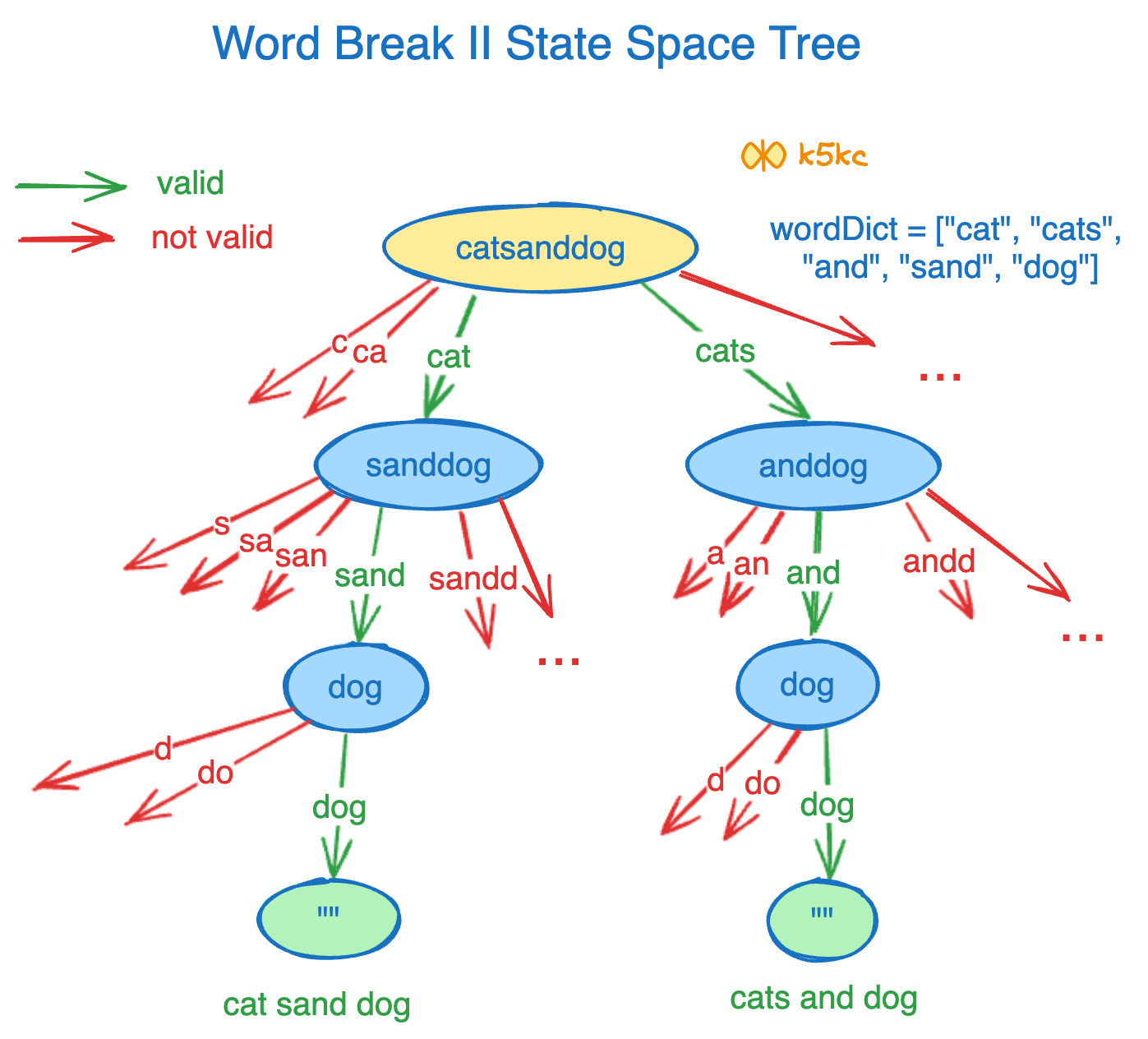
Input: s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"]
Output: ["cats and dog","cat sand dog"]

Example 2:

Input: s = "pineapplepenapple", wordDict = ["apple","pen","applepen","pine","pineapple"]
Output: ["pine apple pen apple","pineapple pen apple","pine applepen apple"]
Explanation: Note that you are allowed to reuse a dictionary word.

Example 3:

Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: []

Solution

We have already seen part 1 of the problem - [Word Break 1 - Check if word is breakable](word-break-1-check-if-word-is-breakable). Instead of using a boolean array to track the matched positions, we need to track the actual matched words.

Method 1 - Backtracking

We have seen [Word Break 1 - Check if word is breakable#Method 2 - Still naive - Try to break the string using all prefixes](word-break-1-check-if-word-is-breakable.md/#method-2---still-naive---try-to-break-the-string-using-all-prefixes). We will use solution similar to [Subsets](subsets-1).

Video Explanation

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/lgcAjEmCGXY" frameborder="0" allowfullscreen></iframe></div>

Code

Java

public class Solution {
	public List<String> wordBreak(String s, List<String> wordDict) {
		List<String> ans = new ArrayList<>();
		dfs(s, new HashSet<String>(wordDict), 0, ans, new ArrayList<>());
        return ans;
	}

	private void dfs(String s, Set<String> set, int idx, List<String> ans, List<String> subAns) {
		if (idx == s.length()) {
			if (subAns.size() > 0) {
				ans.add(String.join(" ", subAns));
			}
			return;
		}
        for(int i = idx + 1; i <= s.length(); i++) {
	        String sub = s.substring(idx,i);
            if(set.contains(sub)) {
	            subAns.add(sub);
	            dfs(s, set, i, ans, subAns);
                subAns.remove(subAns.size() - 1);
            }
        }
	}
}

Complexity

• ⏰ Time complexity: O(2^n)
• 🧺 Space complexity: O(n + m) - where n is the length of string s, and m is number of words in dict

Method 2 - Dynamic Programming

#TODO use DP solution used in [Word Break 1 - Check if word is breakable](word-break-1-check-if-word-is-breakable).

Method 3 - Using Trie

#TODO work on this solution later