Word Search 2 - Return All Words

Problem

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Examples

Example 1:

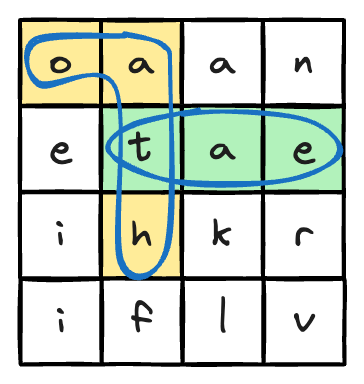
Input:
board = [
	["o","a","a","n"],
	["e","t","a","e"],
	["i","h","k","r"],
	["i","f","l","v"]
], 
words = ["oath","pea","eat","rain"]

Output: 
["eat","oath"]

Similar Problems

Word Search 1

This is a follow up: [Word Search 1 - Find if word exists](word-search-1-find-if-word-exists)

Boggle Solver

Boggle is a game played on a 4 x 4 grid of letters. The goal is to find as many words as possible that can be formed by a sequence of adjacent letters in the grid, using each cell at most once. Given a game board and a dictionary of valid words, implement a Boggle solver.

Key differences:

• Movement: Boggle allows 8 directions (including diagonals), Word Search II uses 4 directions
• Grid size: Boggle is traditionally 4x4, Word Search II can be any m×n
• Word source: Boggle uses a dictionary, Word Search II uses a specific word list
• Minimum length: Boggle typically requires 3+ character words

Examples

Example 1

G I Z E
U E K S  →  Can find: GEEK, QUIZ, SEEK, GUY, ZUKES
Q S E R
A B C D

Solution

Video explanation

Here is the video explaining below methods in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/53EPI8Sp1qY" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Backtracking and DFS

Similar to [Word Search 1 - Find if word exists](word-search-1-find-if-word-exists), this problem can be solved by DFS. However, this solution exceeds time limit.

Intuition

We check each word individually by trying to find it on the board using DFS from every cell. For each word, we perform a fresh search, marking visited cells by modifying a copy of the board. This brute-force approach works but is slow for large boards or word lists.

Approach

1. For each word in words, iterate over every cell in the board as a possible starting point.
2. For each starting cell, perform DFS to try to match the word, marking visited cells by setting them to # in a copy of the board.
3. If the word is found, add it to the answer list and move to the next word.
4. Return the list of found words.

Complexity

• ⏰ Time complexity: O(W * m * n * L) – For each of the W words, we may start a DFS from every cell (m * n), and each DFS can go up to the length of the word L.
• 🧺 Space complexity: O(m * n + L) – We use a copy of the board for each DFS (O(m * n)), and the recursion stack can go up to L.

Code

C++

class Solution {
public:
	std::vector<std::string> findWords(std::vector<std::vector<char>>& board, std::vector<std::string>& words) {
		std::vector<std::string> ans;
		int m = board.size();
		int n = board[0].size();
		for (const std::string& word : words) {
			bool flag = false;
			for (int i = 0; i < m && !flag; ++i) {
				for (int j = 0; j < n && !flag; ++j) {
					std::vector<std::vector<char>> newBoard = board;
					if (dfs(newBoard, word, i, j, 0)) {
						flag = true;
					}
				}
			}
			if (flag) {
				ans.push_back(word);
			}
		}
		return ans;
	}

private:
	bool dfs(std::vector<std::vector<char>>& board, const std::string& word, int i, int j, int k) {
		int m = board.size();
		int n = board[0].size();
		if (i < 0 || j < 0 || i >= m || j >= n || k > (int)word.size() - 1) {
			return false;
		}
		if (board[i][j] == word[k]) {
			char temp = board[i][j];
			board[i][j] = '#';
			if (k == (int)word.size() - 1) {
				return true;
			} else if (dfs(board, word, i - 1, j, k + 1) ||
					   dfs(board, word, i + 1, j, k + 1) ||
					   dfs(board, word, i, j - 1, k + 1) ||
					   dfs(board, word, i, j + 1, k + 1)) {
				board[i][j] = temp;
				return true;
			}
		} else {
			return false;
		}
		return false;
	}
};

Java

class Solution {
	public List<String> findWords(char[][] board, String[] words) {
		List<String> ans = new ArrayList<String>();
		int m = board.length;
		int n = board[0].length;
		for (String word : words) {
			boolean flag = false;
			for (int i = 0; i < m && !flag; i++) {
				for (int j = 0; j < n && !flag; j++) {
					char[][] newBoard = new char[m][n];
					for (int x = 0; x < m; x++) {
						for (int y = 0; y < n; y++) {
							newBoard[x][y] = board[x][y];
						}
					}
					if (dfs(newBoard, word, i, j, 0)) {
						flag = true;
					}
				}
			}
			if (flag) {
				ans.add(word);
			}
		}
		return ans;
	}

	private boolean dfs(char[][] board, String word, int i, int j, int k) {
		int m = board.length;
		int n = board[0].length;
		if (i < 0 || j < 0 || i >= m || j >= n || k > word.length() - 1) {
			return false;
		}
		if (board[i][j] == word.charAt(k)) {
			char temp = board[i][j];
			board[i][j] = '#';
			if (k == word.length() - 1) {
				return true;
			} else if (dfs(board, word, i - 1, j, k + 1) ||
					   dfs(board, word, i + 1, j, k + 1) ||
					   dfs(board, word, i, j - 1, k + 1) ||
					   dfs(board, word, i, j + 1, k + 1)) {
				board[i][j] = temp;
				return true;
			}
		} else {
			return false;
		}
		return false;
	}
}

Python

from typing import List

class Solution:
	def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
		ans = []
		m, n = len(board), len(board[0])
		for word in words:
			flag = False
			for i in range(m):
				for j in range(n):
					new_board = [row[:] for row in board]
					if self.dfs(new_board, word, i, j, 0):
						flag = True
						break
				if flag:
					break
			if flag:
				ans.append(word)
		return ans

	def dfs(self, board: List[List[str]], word: str, i: int, j: int, k: int) -> bool:
		m, n = len(board), len(board[0])
		if i < 0 or j < 0 or i >= m or j >= n or k > len(word) - 1:
			return False
		if board[i][j] == word[k]:
			temp = board[i][j]
			board[i][j] = '#'
			if k == len(word) - 1:
				return True
			elif (self.dfs(board, word, i - 1, j, k + 1) or
				  self.dfs(board, word, i + 1, j, k + 1) or
				  self.dfs(board, word, i, j - 1, k + 1) or
				  self.dfs(board, word, i, j + 1, k + 1)):
				board[i][j] = temp
				return True
		else:
			return False
		return False

Method 2 - Trie-Based DFS with Prefix Pruning and Set-based Deduplication

Intuition

Instead of searching 1 word at a time, we can build a trie from the list of words and search If the current candidate does not exist in all words' prefix, we can stop backtracking immediately. This can be done by using a trie structure. By building a Trie from the list of words, we can efficiently check if a current path is a valid prefix of any word. This allows us to prune the DFS search space early, avoiding unnecessary exploration. We use a set to collect found words and avoid duplicates.

Approach

1. Build a Trie from all words in the list.
2. For each cell in the board, start a DFS search, passing the current prefix and a visited matrix.
3. At each step, check if the current prefix exists in the Trie. If not, backtrack immediately.
4. If the prefix is a complete word in the Trie, add it to the result set.
5. Mark the cell as visited, recursively search in all four directions, then unmark the cell.
6. Return all found words as a list.

Complexity

• ⏰ Time complexity: O(W * L + m * n * 4^L) – Building the Trie takes O(W * L), and in the worst case, DFS explores up to 4^L paths from each cell.
• 🧺 Space complexity: O(W * L + m * n) – The Trie uses O(W * L) space, and the visited matrix uses O(m * n).

Code

C++

#include <vector>
#include <string>
#include <unordered_set>
using namespace std;

struct TrieNode {
	TrieNode* children[26] = {};
	string word = "";
};

class Trie {
public:
	TrieNode* root;
	Trie() { root = new TrieNode(); }
	void insert(const string& word) {
		TrieNode* node = root;
		for (char c : word) {
			int idx = c - 'a';
			if (!node->children[idx]) node->children[idx] = new TrieNode();
			node = node->children[idx];
		}
		node->word = word;
	}
};

class Solution {
public:
	vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
		Trie trie;
		for (const string& word : words) trie.insert(word);
		unordered_set<string> result;
		int m = board.size(), n = board[0].size();
		vector<vector<bool>> visited(m, vector<bool>(n, false));
		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				dfs(board, visited, i, j, trie.root, result);
			}
		}
		return vector<string>(result.begin(), result.end());
	}
private:
	void dfs(vector<vector<char>>& board, vector<vector<bool>>& visited, int i, int j, TrieNode* node, unordered_set<string>& result) {
		int m = board.size(), n = board[0].size();
		if (i < 0 || j < 0 || i >= m || j >= n || visited[i][j]) return;
		char c = board[i][j];
		TrieNode* next = node->children[c - 'a'];
		if (!next) return;
		if (!next->word.empty()) result.insert(next->word);
		visited[i][j] = true;
		dfs(board, visited, i - 1, j, next, result);
		dfs(board, visited, i + 1, j, next, result);
		dfs(board, visited, i, j - 1, next, result);
		dfs(board, visited, i, j + 1, next, result);
		visited[i][j] = false;
	}
};

Java

import java.util.*;

class TrieNode {
	TrieNode[] children = new TrieNode[26];
	String word = "";
}

class Trie {
	TrieNode root = new TrieNode();
	public void insert(String word) {
		TrieNode node = root;
		for (char c : word.toCharArray()) {
			int idx = c - 'a';
			if (node.children[idx] == null) node.children[idx] = new TrieNode();
			node = node.children[idx];
		}
		node.word = word;
	}
}

class Solution {
	public List<String> findWords(char[][] board, String[] words) {
		Trie trie = new Trie();
		for (String word : words) trie.insert(word);
		Set<String> result = new HashSet<>();
		int m = board.length, n = board[0].length;
		boolean[][] visited = new boolean[m][n];
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				dfs(board, visited, i, j, trie.root, result);
			}
		}
		return new ArrayList<>(result);
	}

	private void dfs(char[][] board, boolean[][] visited, int i, int j, TrieNode node, Set<String> result) {
		int m = board.length, n = board[0].length;
		if (i < 0 || j < 0 || i >= m || j >= n || visited[i][j]) return;
		char c = board[i][j];
		TrieNode next = node.children[c - 'a'];
		if (next == null) return;
		if (!next.word.equals("")) result.add(next.word);
		visited[i][j] = true;
		dfs(board, visited, i - 1, j, next, result);
		dfs(board, visited, i + 1, j, next, result);
		dfs(board, visited, i, j - 1, next, result);
		dfs(board, visited, i, j + 1, next, result);
		visited[i][j] = false;
	}
}

Python

from typing import List, Set

class TrieNode:
	def __init__(self):
		self.children = {}
		self.word = ""

class Trie:
	def __init__(self):
		self.root = TrieNode()
	def insert(self, word: str) -> None:
		node = self.root
		for c in word:
			if c not in node.children:
				node.children[c] = TrieNode()
			node = node.children[c]
		node.word = word

class Solution:
	def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
		trie = Trie()
		for word in words:
			trie.insert(word)
		result: Set[str] = set()
		m, n = len(board), len(board[0])
		visited = [[False] * n for _ in range(m)]
		for i in range(m):
			for j in range(n):
				self.dfs(board, visited, i, j, trie.root, result)
		return list(result)

	def dfs(self, board: List[List[str]], visited: List[List[bool]], i: int, j: int, node: TrieNode, result: Set[str]) -> None:
		m, n = len(board), len(board[0])
		if i < 0 or j < 0 or i >= m or j >= n or visited[i][j]:
			return
		c = board[i][j]
		next_node = node.children.get(c)
		if not next_node:
			return
		if next_node.word:
			result.add(next_node.word)
		visited[i][j] = True
		self.dfs(board, visited, i - 1, j, next_node, result)
		self.dfs(board, visited, i + 1, j, next_node, result)
		self.dfs(board, visited, i, j - 1, next_node, result)
		self.dfs(board, visited, i, j + 1, next_node, result)
		visited[i][j] = False

Method 3 - Trie-Optimized DFS with In-Place Board Marking

Intuition

This approach further optimizes the Trie-based DFS by marking found words as null in the Trie to avoid duplicates and by marking visited cells in-place on the board (using #). This eliminates the need for a visited matrix or set, and allows for efficient pruning of the search space.

Approach

1. Build a Trie from all words.
2. For each cell in the board, start DFS with the root of the Trie.
3. At each DFS step, if the current Trie node contains a word, add it to the answer and set the word to null to avoid duplicates.
4. Mark the current cell as visited by setting it to #.
5. Recursively search in all four directions.
6. Restore the cell after DFS.
7. Optionally, prune Trie branches when all children are null.

Complexity

• ⏰ Time complexity: O(W * L + m * n * 4^L) – Building the Trie takes O(W * L), and DFS explores up to 4^L paths from each cell.
• 🧺 Space complexity: O(W * L) – The Trie uses O(W * L) space; no extra visited matrix is needed.

Code

C++

#include <vector>
#include <string>
using namespace std;

struct TrieNode {
	TrieNode* children[26] = {};
	string word = "";
};

class Trie {
public:
	TrieNode* root;
	Trie() { root = new TrieNode(); }
	void insert(const string& word) {
		TrieNode* node = root;
		for (char c : word) {
			int idx = c - 'a';
			if (!node->children[idx]) node->children[idx] = new TrieNode();
			node = node->children[idx];
		}
		node->word = word;
	}
};

class Solution {
public:
	vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
		Trie trie;
		for (const string& word : words) trie.insert(word);
		vector<string> ans;
		int m = board.size(), n = board[0].size();
		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				dfs(board, i, j, trie.root, ans);
			}
		}
		return ans;
	}
private:
	void dfs(vector<vector<char>>& board, int i, int j, TrieNode* node, vector<string>& ans) {
		int m = board.size(), n = board[0].size();
		if (i < 0 || j < 0 || i >= m || j >= n) return;
		char c = board[i][j];
		if (c == '#' || !node->children[c - 'a']) return;
		node = node->children[c - 'a'];
		if (!node->word.empty()) {
			ans.push_back(node->word);
			node->word = ""; // Avoid duplicates
		}
		board[i][j] = '#';
		dfs(board, i + 1, j, node, ans);
		dfs(board, i - 1, j, node, ans);
		dfs(board, i, j + 1, node, ans);
		dfs(board, i, j - 1, node, ans);
		board[i][j] = c;
	}
};

Java

class TrieNode {
    TrieNode[] children = new TrieNode[26];
    String word;
}

class Trie {
    TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    public void insert(String word) {
        TrieNode curr = root;
        for (char c : word.toCharArray()) {
            int i = c - 'a';
            if (curr.children[i] == null) {
                curr.children[i] = new TrieNode();
            }
            curr = curr.children[i];
        }
        curr.word = word;
    }
}

class Solution {
    public List<String> findWords(char[][] board, String[] words) {
        Trie trie = new Trie();
        for (String word : words) {
            trie.insert(word);
        }

        List<String> ans = new ArrayList<>();
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                dfs(board, i, j, trie.root, ans);
            }
        }
        return ans;
    }

    private void dfs(char[][] board, int i, int j, TrieNode p, List<String> ans) {
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) {
            return;
        }
        char ch = board[i][j];
        if (ch == '#' || p.children[ch - 'a'] == null) {
            return;
        }

        p = p.children[ch - 'a'];
        if (p.word != null) {
            ans.add(p.word);
            p.word = null; // Avoid duplicates
        }

        board[i][j] = '#';
        dfs(board, i + 1, j, p, ans);
        dfs(board, i - 1, j, p, ans);
        dfs(board, i, j + 1, p, ans);
        dfs(board, i, j - 1, p, ans);
        board[i][j] = ch;
    }
}

Python

class TrieNode:
    def __init__(self):
        self.children: dict[str, TrieNode] = {}
        self.word: str | None = None

class Trie:
    def __init__(self):
        self.root = TrieNode()

    def insert(self, word: str) -> None:
        curr = self.root
        for c in word:
            if c not in curr.children:
                curr.children[c] = TrieNode()
            curr = curr.children[c]
        curr.word = word

class Solution:
    def findWords(self, board: list[list[str]], words: list[str]) -> list[str]:
        trie = Trie()
        for word in words:
            trie.insert(word)

        ans = []
        m, n = len(board), len(board[0])

        def dfs(i: int, j: int, node: TrieNode):
            if not (0 <= i < m and 0 <= j < n and board[i][j] != '#'):
                return

            ch = board[i][j]
            curr_node = node.children.get(ch)

            if not curr_node:
                return

            if curr_node.word:
                ans.append(curr_node.word)
                curr_node.word = None  # Avoid duplicates
            
            board[i][j] = '#'

            dfs(i + 1, j, curr_node)
            dfs(i - 1, j, curr_node)
            dfs(i, j + 1, curr_node)
            dfs(i, j - 1, curr_node)
            
            board[i][j] = ch
            
            if not curr_node.children:
                node.children.pop(ch)

        for i in range(m):
            for j in range(n):
                dfs(i, j, trie.root)
        
        return ans