Zigzag Grid Traversal With Skip
EasyUpdated: Aug 2, 2025
Practice on:
Problem
You are given an m x n 2D array grid of positive integers.
Your task is to traverse grid in a zigzag pattern while skipping every
alternate cell.
Zigzag pattern traversal is defined as following the below actions:
- Start at the top-left cell
(0, 0). - Move right within a row until the end of the row is reached.
- Drop down to the next row, then traverse left until the beginning of the row is reached.
- Continue alternating between right and left traversal until every row has been traversed.
Note that you must skip every alternate cell during the traversal.
Return an array of integers result containing, in order , the value of the cells visited during the zigzag traversal with skips.
Examples
Example 1
Input: grid = [[1,2],[3,4]]
Output: [1,4]
Explanation:
**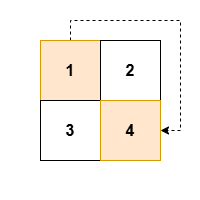**
Example 2
Input: grid = [[2,1],[2,1],[2,1]]
Output: [2,1,2]
Explanation:
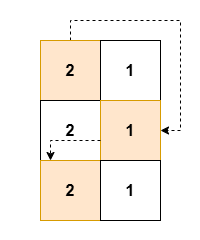
Example 3
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,3,5,7,9]
Explanation:
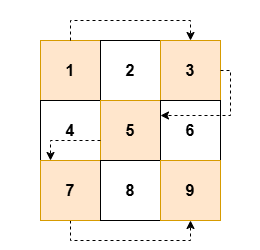
Constraints
2 <= n == grid.length <= 502 <= m == grid[i].length <= 501 <= grid[i][j] <= 2500
Solution
Method 1 – Simulation with Zigzag Indexing
Intuition
The main idea is to simulate the zigzag traversal row by row, alternating direction, and skip every alternate cell by toggling a flag. We only add a cell to the result if it is not skipped.
Approach
- Initialize an empty result array and a skip flag set to False.
- For each row in the grid:
- If the row index is even, traverse left to right; if odd, traverse right to left.
- For each cell in the current row (in the correct direction):
- If skip is False, add the cell to the result.
- Toggle the skip flag after each cell.
- Return the result array after traversing all rows.
Code
C++
class Solution {
public:
vector<int> zigzagTraversal(vector<vector<int>>& grid) {
vector<int> ans;
bool skip = false;
int n = grid.size(), m = grid[0].size();
for (int i = 0; i < n; ++i) {
if (i % 2 == 0) {
for (int j = 0; j < m; ++j) {
if (!skip) ans.push_back(grid[i][j]);
skip = !skip;
}
} else {
for (int j = m - 1; j >= 0; --j) {
if (!skip) ans.push_back(grid[i][j]);
skip = !skip;
}
}
}
return ans;
}
};
Go
func zigzagTraversal(grid [][]int) []int {
n, m := len(grid), len(grid[0])
ans := []int{}
skip := false
for i := 0; i < n; i++ {
if i%2 == 0 {
for j := 0; j < m; j++ {
if !skip {
ans = append(ans, grid[i][j])
}
skip = !skip
}
} else {
for j := m - 1; j >= 0; j-- {
if !skip {
ans = append(ans, grid[i][j])
}
skip = !skip
}
}
}
return ans
}
Java
class Solution {
public List<Integer> zigzagTraversal(int[][] grid) {
List<Integer> ans = new ArrayList<>();
boolean skip = false;
int n = grid.length, m = grid[0].length;
for (int i = 0; i < n; i++) {
if (i % 2 == 0) {
for (int j = 0; j < m; j++) {
if (!skip) ans.add(grid[i][j]);
skip = !skip;
}
} else {
for (int j = m - 1; j >= 0; j--) {
if (!skip) ans.add(grid[i][j]);
skip = !skip;
}
}
}
return ans;
}
}
Kotlin
class Solution {
fun zigzagTraversal(grid: Array<IntArray>): List<Int> {
val ans = mutableListOf<Int>()
var skip = false
val n = grid.size
val m = grid[0].size
for (i in 0 until n) {
if (i % 2 == 0) {
for (j in 0 until m) {
if (!skip) ans.add(grid[i][j])
skip = !skip
}
} else {
for (j in m - 1 downTo 0) {
if (!skip) ans.add(grid[i][j])
skip = !skip
}
}
}
return ans
}
}
Python
from typing import List
class Solution:
def zigzagTraversal(self, grid: List[List[int]]) -> List[int]:
ans: List[int] = []
skip = False
n, m = len(grid), len(grid[0])
for i in range(n):
rng = range(m) if i % 2 == 0 else range(m-1, -1, -1)
for j in rng:
if not skip:
ans.append(grid[i][j])
skip = not skip
return ans
Rust
impl Solution {
pub fn zigzag_traversal(grid: Vec<Vec<i32>>) -> Vec<i32> {
let n = grid.len();
let m = grid[0].len();
let mut ans = Vec::new();
let mut skip = false;
for i in 0..n {
if i % 2 == 0 {
for j in 0..m {
if !skip {
ans.push(grid[i][j]);
}
skip = !skip;
}
} else {
for j in (0..m).rev() {
if !skip {
ans.push(grid[i][j]);
}
skip = !skip;
}
}
}
ans
}
}
TypeScript
class Solution {
zigzagTraversal(grid: number[][]): number[] {
const ans: number[] = [];
let skip = false;
const n = grid.length, m = grid[0].length;
for (let i = 0; i < n; i++) {
const rng = i % 2 === 0 ? [...Array(m).keys()] : Array.from({length: m}, (_, k) => m - 1 - k);
for (const j of rng) {
if (!skip) ans.push(grid[i][j]);
skip = !skip;
}
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n*m)— We visit each cell in the grid once, toggling the skip flag, so the work is proportional to the number of cells. - 🧺 Space complexity:
O(n*m)— The result array can contain up to half the cells in the grid in the worst case.