Construct Binary Tree from Inorder and Preorder Traversal

Problem

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Examples

Example 1:

	3
   / \
  9   20
	 /  \
	15   7

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Solution

Video explanation

Here is the video explaining this method in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/v2Nhmp3YU1U" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Recursive Divide and Conquer

Lets look at the binary tree:

         1
        / \
       2   3
      / \ / \
     4  5 6  7

The inorder and preorder traversal are:

inorder = [4, 2, 5, 1, 6, 3, 7]
preorder = [1, 2, 4, 5, 3, 6, 7]

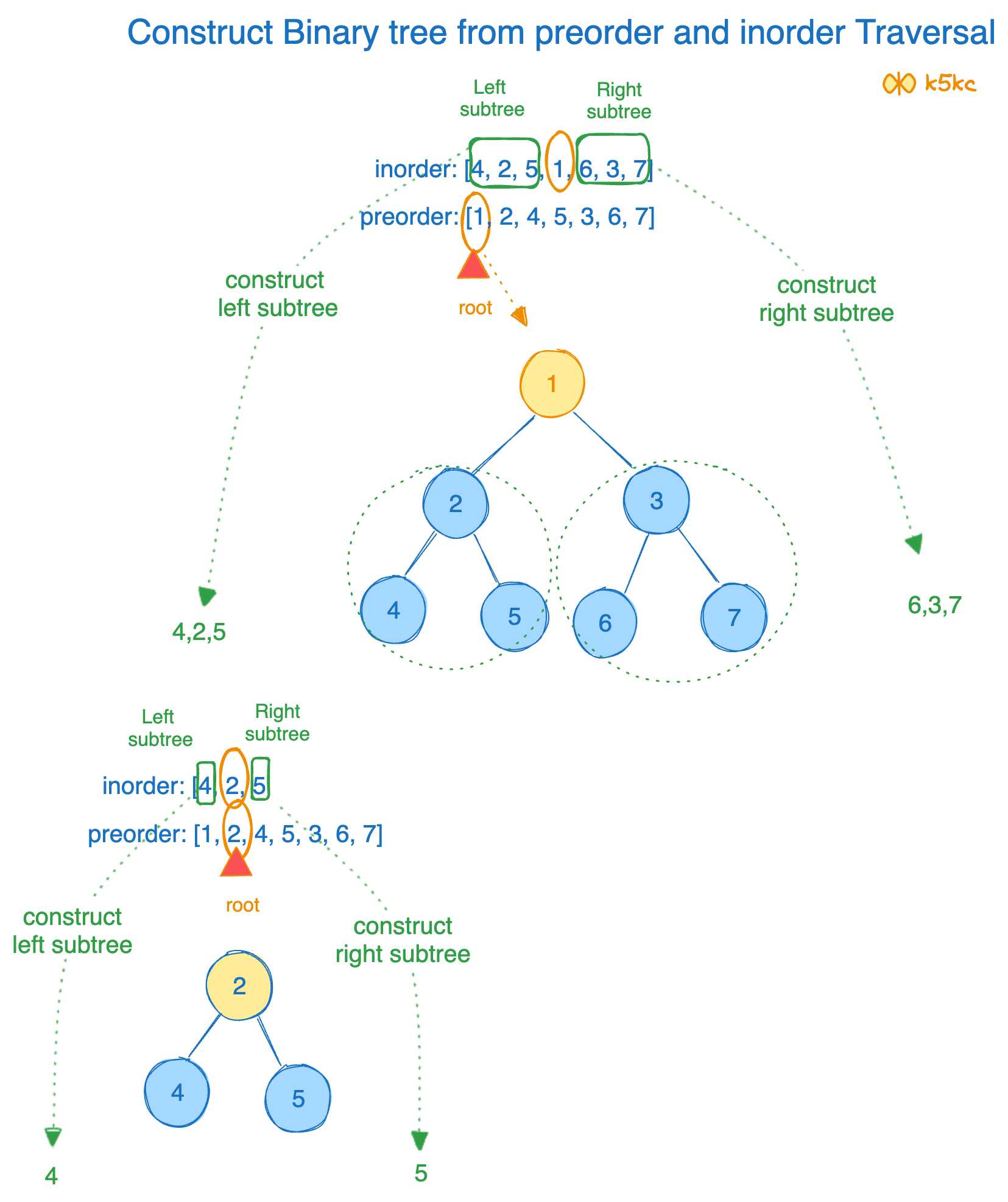
How does preorder[] array helps? The first element in preorder[] acts as the root of the tree (in this case, 1).

How does inorder[] array helps? inorder[] helps determine the left and right subtrees of the root. Elements appearing before the root in inorder[] belong to the left subtree, while elements appearing after belong to the right subtree. In our case, it is [4, 2, 5] on left and [6, 3, 7] on right. (See picture below).

See this step above and recursively construct left subtree and link it root.left and recursively construct right subtree and link it root.right.

Code

Java

class Solution {
    private int[] preorder;
    private int[] inorder;

	public TreeNode buildTree(int[] preorder, int[] inorder) {
		if (preorder == null || preorder.length == 0 || inorder.length == 0 || preLength != inLength) {
			return null;
		}
		
		// We use indices to pass subarrays, which is more efficient than copying arrays on each call.
        this.preorder = preorder;
        this.inorder = inorder;
	
		int preLength = preorder.length;
		int inLength = inorder.length;
		return helper(preorder, inorder, 0, 0, inLength - 1);
	}
	
	private TreeNode helper(int preStart, int inStart, int inEnd) {
		if (inStart > inEnd || preStart > preorder.length - 1) {
			return null;
		}
	
		// Pick current node from Preorder traversal using preStart and increment preStart
		TreeNode root = new TreeNode(preorder[preStart]);
	
		// If this node has no children then return
		if (inStart == inEnd) {
			return root;
		}
	
		// Else find the index of this node in Inorder traversal
		int inIndex = linearSearch(inorder, root.val, inStart, inEnd);
	
		// Using index in Inorder traversal, construct left and right subtrees
		root.left = helper(preStart + 1, inStart, inIndex - 1);
		// We are skipping the elements on the left of the current pre order node by adding inIndex - inStart + 1
		root.right = helper(preStart + inIndex - inStart + 1, inIndex + 1, inEnd);
	
		return root;
	}
	
	
	static int linearSearch(int[] arr, int value, int start, int end) {
		for (int i = start; i <= end; i++) {
			if (arr[i] == value) {
				return i;
			}
		}
		return -1;
	}
}

Python

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        if not preorder or not inorder:
            return None

        root_val = preorder[0]
        root = TreeNode(root_val)

        # This O(n) scan is the bottleneck
        inorder_root_index = inorder.index(root_val)

        # List slicing is inefficient for each recursive call
        left_inorder = inorder[:inorder_root_index]
        right_inorder = inorder[inorder_root_index + 1:]

        left_preorder = preorder[1:1 + len(left_inorder)]
        right_preorder = preorder[1 + len(left_inorder):]

        root.left = self.buildTree(left_preorder, left_inorder)
        root.right = self.buildTree(right_preorder, right_inorder)

        return root

Complexity

• ⏰ Time complexity: O(n^2) in the implementation shown above that uses linearSearch to locate the root in the inorder array. In the worst case (skewed trees), each recursive step performs an O(n) scan which leads to a quadratic total cost.
  • Optimized variant: O(n) if you precompute a hash map from value → inorder index before recursion; then each node is created and positioned in O(1) work.
• 🧺 Space complexity: O(n) total. The output tree stores n nodes; recursion stack uses O(h) auxiliary space where h is the tree height (worst-case O(n) for a skewed tree). The optimized variant additionally requires O(n) space for the index map.

Method 2 - Recursive Divide and Conquer with Inorder Index Mapping

Intuition

The naive approach has two main bottlenecks: the O(n) linear scan to find the root in the inorder array, and (in some implementations) the O(k) cost of slicing arrays at each step. We can eliminate both.

• The problem states that all values are unique. This is the key that allows us to use a hash map to store the indices of the inorder elements, turning our O(n) search into an O(1) lookup.
• To eliminate the slicing cost, we use indices to define the boundaries of our current subproblem for both arrays, ensuring we don't create new arrays in memory.

Approach

1. First, make a single pass through the inorder array to build a hash map (inorder_map) that maps each element's value to its index.
2. Create a recursive helper function that takes indices as arguments (preStart, inStart, inEnd) to define the current subproblem.
3. In the helper, the current root is preorder[preStart].
4. Use the inorder_map to find the root's index (inIndex) in O(1) time.
5. Calculate the size of the left subtree: leftSubtreeSize = inIndex - inStart.
6. Make two recursive calls, calculating the new index boundaries for each:
   • Left child: The preorder starts at preStart + 1, and the inorder segment is from inStart to inIndex - 1.
   • Right child: The preorder starts at preStart + 1 + leftSubtreeSize, and the inorder segment is from inIndex + 1 to inEnd.
7. This approach processes each node once with O(1) work for the lookup, resulting in an optimal O(n) time complexity.

Complexity

• ⏰ Time complexity: O(n). For each node in preorder finding its index in inorder now just takes O(n) time.
• 🧺 Space complexity: O(n) for recursion stack and hashmap to store inorder indices.

Code

Java

class Solution {
    private int[] preorder;
    private Map<Integer, Integer> inorderMap;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        this.inorderMap = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            this.inorderMap.put(inorder[i], i);
        }
        return helper(0, 0, inorder.length - 1);
    }

    private TreeNode helper(int preStart, int inStart, int inEnd) {
        // Base case
        if (inStart > inEnd) {
            return null;
        }

        // The root is the first element in the current preorder segment
        int rootVal = this.preorder[preStart];
        TreeNode root = new TreeNode(rootVal);

        // Find root's index in O(1) using the map
        int inIndex = this.inorderMap.get(rootVal);
        
        // Calculate the size of the left subtree
        int leftSubtreeSize = inIndex - inStart;

        // Recursive calls are now identical in structure to the naive version
        root.left = helper(preStart + 1, inStart, inIndex - 1);
        root.right = helper(preStart + 1 + leftSubtreeSize, inIndex + 1, inEnd);
        
        return root;
    }
}

Python

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        self.preorder = preorder
        self.inorder_map = {val: i for i, val in enumerate(inorder)}
        
        return self.build_helper(0, 0, len(inorder) - 1)

    def build_helper(self, pre_start: int, in_start: int, in_end: int) -> Optional[TreeNode]:
        # Base case
        if in_start > in_end:
            return None
        
        # The root is the first element in the current preorder segment
        root_val = self.preorder[pre_start]
        root = TreeNode(root_val)
        
        # Find root's index in O(1) using the map
        in_index = self.inorder_map[root_val]

        # Calculate the size of the left subtree
        left_subtree_size = in_index - in_start
        
        # Recursive calls are now identical in structure to the naive version
        root.left = self.build_helper(pre_start + 1, in_start, in_index - 1)
        root.right = self.build_helper(pre_start + 1 + left_subtree_size, in_index + 1, in_end)
        
        return root