Problem

You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

We define the right direction as positive x-axis (increasing x-coordinate) and the left direction as negative x-axis (decreasing x-coordinate). Similarly, we define the up direction as positive y-axis (increasing y-coordinate) and the down direction as negative y-axis (decreasing y-coordinate)

You have to place n people, including Alice and Bob, at these points such that there is exactly one person at every point. Alice wants to be alone with Bob, so Alice will build a rectangular fence with Alice’s position as the upper left corner and Bob’s position as the lower right corner of the fence (Note that the fence might not enclose any area, i.e. it can be a line). If any person other than Alice and Bob is either inside the fence or on the fence, Alice will be sad.

Return the number ofpairs of points where you can place Alice and Bob, such that Alice does not become sad on building the fence.

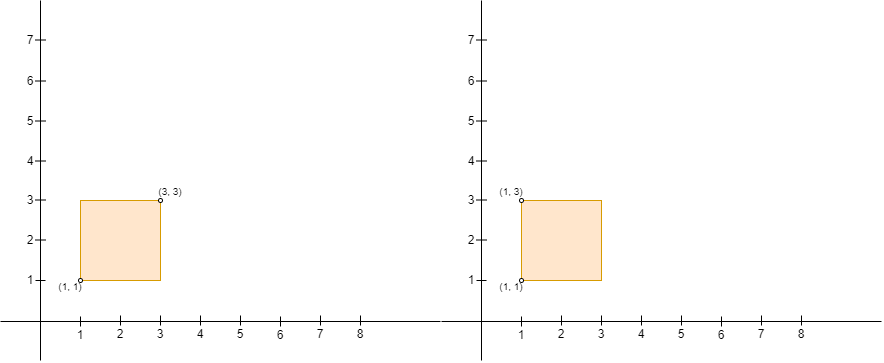
Note that Alice can only build a fence with Alice’s position as the upper left corner, and Bob’s position as the lower right corner. For example, Alice cannot build either of the fences in the picture below with four corners (1, 1), (1, 3), (3, 1), and (3, 3), because:

  • With Alice at (3, 3) and Bob at (1, 1), Alice’s position is not the upper left corner and Bob’s position is not the lower right corner of the fence.
  • With Alice at (1, 3) and Bob at (1, 1), Bob’s position is not the lower right corner of the fence.

Examples

Example 1

1
2
3

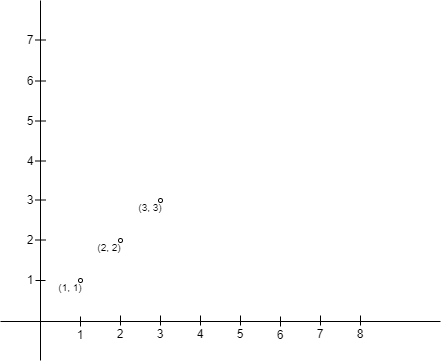
Input: points = [[1,1],[2,2],[3,3]]
Output: 0
Explanation: There is no way to place Alice and Bob such that Alice can build a fence with Alice's position as the upper left corner and Bob's position as the lower right corner. Hence we return 0.

Example 2

1
2
3
4
5
6

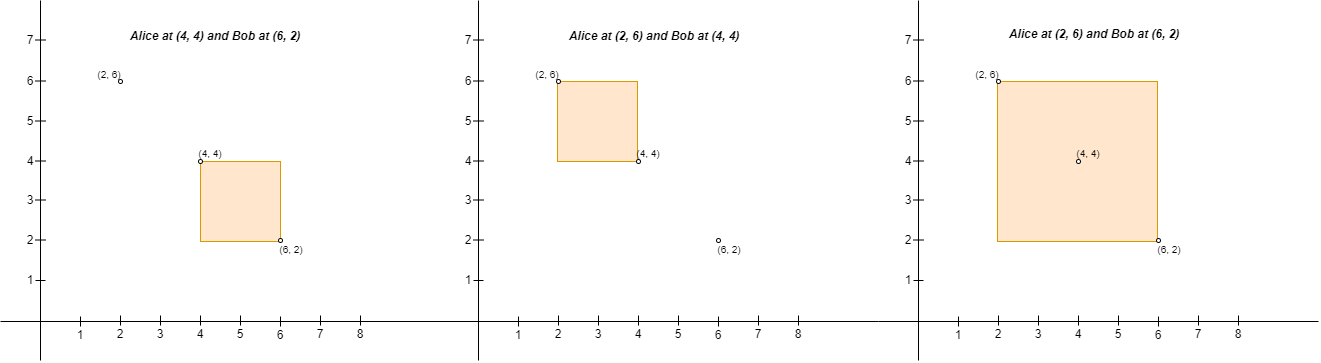
Input: points = [[6,2],[4,4],[2,6]]
Output: 2
Explanation: There are two ways to place Alice and Bob such that Alice will not be sad:
- Place Alice at (4, 4) and Bob at (6, 2).
- Place Alice at (2, 6) and Bob at (4, 4).
You cannot place Alice at (2, 6) and Bob at (6, 2) because the person at (4, 4) will be inside the fence.

Example 3

1
2
3
4
5
6
7

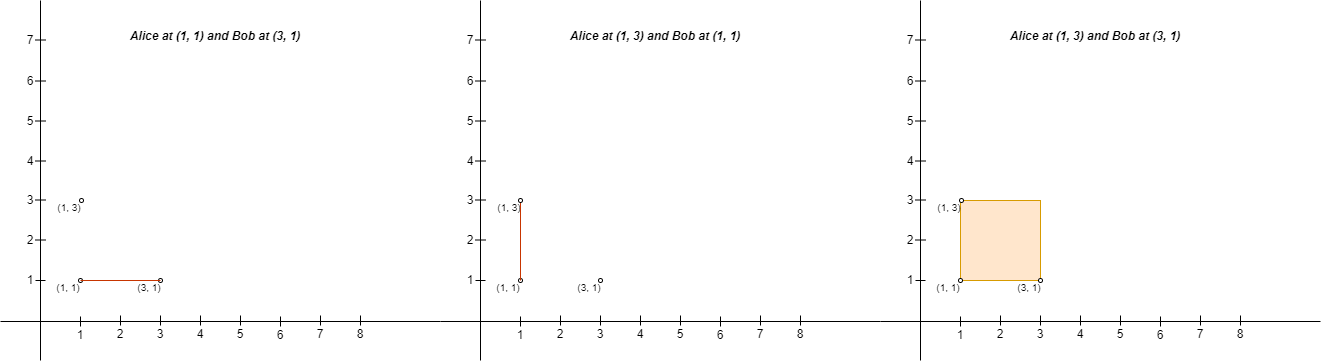
Input: points = [[3,1],[1,3],[1,1]]
Output: 2
Explanation: There are two ways to place Alice and Bob such that Alice will not be sad:
- Place Alice at (1, 1) and Bob at (3, 1).
- Place Alice at (1, 3) and Bob at (1, 1).
You cannot place Alice at (1, 3) and Bob at (3, 1) because the person at (1, 1) will be on the fence.
Note that it does not matter if the fence encloses any area, the first and second fences in the image are valid.

Constraints

  • 2 <= n <= 1000
  • points[i].length == 2
  • -109 <= points[i][0], points[i][1] <= 10^9
  • All points[i] are distinct.
Similar Problems

Solution

Method 1 – Brute Force Rectangle Check

We have covered naive solution Find the Number of Ways to Place People I#Method 1 – Brute Force Rectangle Check here. And it doesn’t give TLE yet. So, we can use that as well for simplicity, but the time complexity is O(n^3).

Method 2 – Sort and Sweep Line (Greedy)

Intuition

By sorting the points by x-coordinate (and y descending for tie-break), we can efficiently count valid pairs using a greedy sweep. For each point (x1, y1), we look at all points to its right (x2, y2) with y1 ≥ y2. Since the points are sorted, x1 ≤ x2 always holds. We keep track of the largest y2 seen so far; if y2 is greater than this, then (x1, y1) and (x2, y2) are alone in their rectangle, and we count the pair.

Approach

  1. Sort all points by x ascending, then y descending.
  2. For each point (x1, y1):
    • Initialize y = -∞ (the lowest possible value).
    • For each point (x2, y2) to the right of (x1, y1):
      • If y1 ≥ y2 > y, count the pair and update y = y2.
  3. Return the total count.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include <algorithm>
#include <vector>
#include <limits>
using namespace std;
class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        int n = points.size(), ans = 0;
        sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
            if (a[0] != b[0]) return a[0] < b[0];
            return a[1] > b[1];
        });
        for (int i = 0; i < n; ++i) {
            int y = numeric_limits<int>::min();
            for (int j = i + 1; j < n; ++j) {
                if (points[i][1] >= points[j][1] && points[j][1] > y) {
                    ans++;
                    y = points[j][1];
                }
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

import "sort"
import "math"
func numberOfPairs(points [][]int) int {
    n := len(points)
    sort.Slice(points, func(i, j int) bool {
        if points[i][0] != points[j][0] {
            return points[i][0] < points[j][0]
        }
        return points[i][1] > points[j][1]
    })
    ans := 0
    for i := 0; i < n; i++ {
        y := math.MinInt32
        for j := i + 1; j < n; j++ {
            if points[i][1] >= points[j][1] && points[j][1] > y {
                ans++
                y = points[j][1]
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public int numberOfPairs(int[][] points) {
        int n = points.length, ans = 0;
        Arrays.sort(points, (a, b) -> a[0] != b[0] ? a[0] - b[0] : b[1] - a[1]);
        for (int i = 0; i < n; ++i) {
            int y = Integer.MIN_VALUE;
            for (int j = i + 1; j < n; ++j) {
                if (points[i][1] >= points[j][1] && points[j][1] > y) {
                    ans++;
                    y = points[j][1];
                }
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    fun numberOfPairs(points: Array<IntArray>): Int {
        points.sortWith(compareBy({ it[0] }, { -it[1] }))
        var ans = 0
        for (i in points.indices) {
            var y = Int.MIN_VALUE
            for (j in i + 1 until points.size) {
                if (points[i][1] >= points[j][1] && points[j][1] > y) {
                    ans++
                    y = points[j][1]
                }
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution:
    def numberOfPairs(self, points: list[list[int]]) -> int:
        ans = 0
        points.sort(key=lambda p: (p[0], -p[1]))
        for i, (x1, y1) in enumerate(points):
            y = float('-inf')
            for x2, y2 in points[i+1:]:
                if y1 >= y2 > y:
                    ans += 1
                    y = y2
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

impl Solution {
    pub fn number_of_pairs(points: Vec<Vec<i32>>) -> i32 {
        let mut pts = points;
        pts.sort_by(|a, b| if a[0] != b[0] { a[0].cmp(&b[0]) } else { b[1].cmp(&a[1]) });
        let n = pts.len();
        let mut ans = 0;
        for i in 0..n {
            let mut y = i32::MIN;
            for j in (i+1)..n {
                if pts[i][1] >= pts[j][1] && pts[j][1] > y {
                    ans += 1;
                    y = pts[j][1];
                }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
    numberOfPairs(points: number[][]): number {
        points.sort((a, b) => a[0] - b[0] || b[1] - a[1]);
        const n = points.length;
        let ans = 0;
        for (let i = 0; i < n; ++i) {
            let y = Number.MIN_SAFE_INTEGER;
            for (let j = i + 1; j < n; ++j) {
                if (points[i][1] >= points[j][1] && points[j][1] > y) {
                    ans++;
                    y = points[j][1];
                }
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2) — For each point, we check all points to its right.
  • 🧺 Space complexity: O(1) — Only a few variables for counting and iteration.